zbiór wartości funkcji i wykres Misiek w potrzebie : Czy znajdzie się jakiś miły człowiek , który mi pomoże ? Zbiór wartości sinx− cosx +1 4 sin²x − 3 cosx +5 Oraz wykresik : sinx* moduł sinx + cosx * moduł cosx Będę wdzięczny za każdą pomoc

ZKS:

	π
sin(x) − cos(x) = √2sin(x −		)
	4

	π		π
f(x) = √2sin(x −		) + 1 zróbmy podstawienie x −		= t
	4		4

−1 < sin(t) < 1 / * √2 −√2 < √2sin(t) < √2 / + 1 −√2 + 1 < √2sin(t) + 1 < √2 + 1

	π
−√2 + 1 < √2sin(x −		) + 1 < √2 + 1
	4

Tak więc zbiór wartości f(x) wynosi [−√2 + 1 ; √2 + 1].

Misiek w potrzebie: A czy ktoś jest mi w stanie pomóc z wykresem bo totalnie nie wiem jak się do tego zabrać

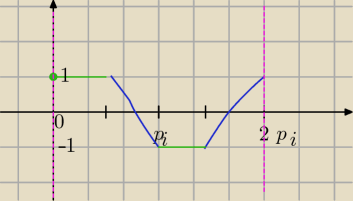
Mila: f(x)=sinx* |sinx| + cosx * | cosx | x∊<0;2π> Narysuj w jednym ukladzie wsp. wykres funkcji y=sinx i y=cosx 1) |sinx|=sinx dla x∊<0;π> |sinx|=−sinx dla x∊<π;2π>

	π		3π
2) |cosx|=cosx dla x∊<0'		)∪<(		;2π}
	2		2

	π		3π
|cosx|=−cosx dla x∊(		;		}
	2		2

	π
a) x∊<0;		)
	2

f(x)=sinx*sinx+cosx*cosx=1

	π
b) x∊(		;π)
	2

f(x)=sin²x−cos²x=−cos2x

	3π
c)x∊<π;		)
	2

f(x)=−sin²x−cos²x=−1

	3π
d) x∊(		;2π>
	2

f(x)=−sinx²+cos²x=cos2x wykres trochę mało dokładny. Popatrz tu:http://www.jogle.pl/wykresy/

Aga1.:

	π
np. dla x∊<0,		)
	2

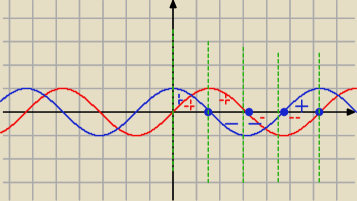
Zauważ,że funkcje sinus i cosinus są okresowe, o okresie podstawowym T=2π IsinxI=sinx i i IcosxI=cosx f(x)=sin²x+cos²x=1

	π
Dla x∊<		,π)
	2

IsinxI=sinx, IcosxI=−cosx f(x)=sin²x−cos²x=−(c0s²x−sin²x)=−cos2x

	3
Gdy x∊<π,		π)
	2

IsinxI=−sinx, i IcosxI=−cosx f(x)=...

	3
Gdy x∊<		π,2π)
	2

ISinxI=−sinx, IcosxI=cosx f(x)=

misiek w potrzebie: Dziękuję !