Oblicz objętość i pole powierzchni otrzymanej bryły. Azo: Oblicz objętość i pole powierzchni otrzymanej bryły. Kwadrat o przekątnej długości 5√2 cm obraca się wokół jednego z boków. Oblicz jego objętość i pole powierzchni tak otrzymanej bryły. Rozwiązałem to tak, czy jest dobrze? Pole podstawy : πr², czyli π25 V = Pole podstawy x wysokość V = 25π x 5 = 125π [j³] Pole powierzchni bocznej : 2πrH, czyli 2π x 5 x 5 = 2π x 25 = 50 π Pole pow. calkowitej: 2 pole podstawy x Pb Ppc = (2 x 25π) x 50 π = 50π x 50π = 2500π² Tak ma być?

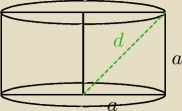
dero2005: d = 5√2

	d√2		5√2*√2
r = h = a =		=		= 5
	2		2

P_c = 2πr² + 2πrh = 2πr(r+h) = 2π*5(5+5) = 100π cm² V = πr²*h = π*5²*5 = 125π cm³ Błąd masz w ostatnim wzorze (nie razy tylko dodać)