zbiór wartości funkcji xzy: Słuchajcie, mam takie oto zadanie: Wyznacz zbiór wartości funkcji. I pierwszy przykład: y=−sin²x+4sinx+12 Więc zrobiłam tak: sinx=t ⋀ t∊ <−1,1> i policzyłam wartości dla −1 i 1. Wyszło zgodnie z odpowiedzią. ale mam drugi przykład: y=cos²x−cos2x−2 cos2x=t ⋀ t∊<−1,1> ale jeżeli zrobię tak, ja w pierwszym przykładzie to wychodzi inaczej niż w odpowiedziach..

krystek: przecież masz cosx jeszcze ! musisz doprowadzić do tych samych argumentów

xzy: pomyłka w pisaniu.. ten drugi przykład jest taki: y=cos²2x−cos2x−2 więc argumenty są takei same

Kejt: t²−t−2=0 Δ=9 t₁=−1 t₂=2 → nie spełnia założenia tak Ci wyszło?

ZKS: Zbiór wartości trzeba wyznaczyć a nie policzyć miejsca zerowe.

Kejt: aa.. ja jak zwykle przytomna jestem

ZKS: To zrób Kejt zadanko.

Kejt: i mnie wkopał

ZKS: Wcale nie wkopał.

Kejt: wcale tak!

ZKS: Skoro tak to mogę ja zrobić żeby nie było że Ci wkopałem.

Kejt: nie wiem dokładnie jak to zrobić

ZKS: Tak jak xyz robił tylko że zapomniał o bardzo ważnej jednej rzeczy przy wyznaczaniu zbioru wartości funkcji.

Kejt: a jk akurat mam o niej pamiętać?

Kejt: ja*

ZKS: Na pewno pamiętasz i wiesz o co chodzi. Co jest potrzebne aby znaleźć wartość maksymalną minimalną w funkcji kwadratowej?

Kejt: aa.. rysunek i wsp. wierzchołka , tak?

asdf: wsp kierunkowy i q

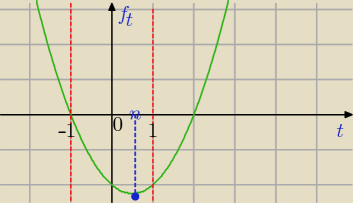
Mila: y=cos²2x−cos2x−2 cos(2x) =t i t∊<−1;1> y=t²−t−2 (rozważamy wykres dla t∊<−1;1>) 1) Wartość najmniejsza badam, czy wierzchołek paraboli należy do dziedziny

	1		1		1		1
tw=		∊<−1;1> ⇔y=(		)2−		−2=−2		jest wartością najmniejszą
	2		2		2		4

wartość największa znajduje się na końcu przedziału y=(−1)²+1−2=0 (bez rysunku, wnioskujesz w którym, albo obliczasz dla 1 i −1 a następnie wybierasz.)

ZKS: I to co napisał asdf współczynnik przy najwyższej potędze wtedy będziemy wiedzieli czy jest to maksimum czy minimum.

Kejt: a..no to ja to miałam na myśli pod "rysunkiem"..