Stereometria kkkkkk: Przekątna prostopadłoscianu tworzy z jego krawędziami kąty: α, β, γ. Wykaż, że sin²α + sin²β + sin²γ = 2

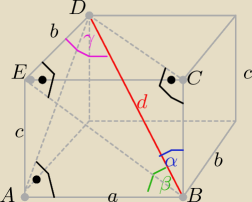
Eta: Trójkąty ABE i BED i BCD są prostokątne i d=√a²+b²+c²

	c		c2
cosα=		⇒ cos2α=
	d		a2+b2+c2

	a		a2
cosβ =		⇒ cos2β=
	d		a2+b2+c2

	b		b2
cosγ=		⇒ cos2γ=
	d		a2+b2+c2

+ −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− cos²α+ cos²β+cos²γ= 1 1−sin²α+1−sin²β+1−sin²γ=1 ⇒ sin²α+sin²β+sin²γ=2 c.n.u