licze na pomoc-planimetria :) paula: 1. Na kole o promieniu 2 opisano trapez równoramienny o kącie ostrym 75stopni. Oblicz pole i obwód tego trapezu. 2. W okrąg o promieniu 3 wpisano czworokąt. Jedna z przekątnych tego czworokąta jest średnicą okręgu, a jeden z jego kątów ma miarę 135stopni. Oblicz długośc drugiej przekatnej tego czworokata. Prosze o rysunk i tłumaczenie jakby można byłoi!

Eta: Pomagam

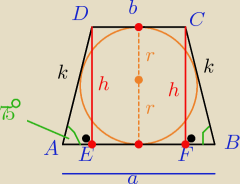
Eta: Witam Jeżeli trapez jest opisany na okręgu, to sumy długości boków przeciwległych są równe więc : a + b = 2k to: Ob= a +b + 2k => Ob= 4k pole trapezu:

	a+b		2k
P=		*h to P=		*h
	2		2

to: P= k*h zatem: skoro r= 2 => h= 2r => h= 4 pozostaje więc tylko wyliczyć długość k z trójkata prostokatnego AED z funkcji tryg. mamy:

	h
		= sin75o
	k

to:

	h
k=
	sin75o

	4
k=
	sin75o

pozostaje odczytać z tablic sin75^o w przybliżeniu lub policzyć dokładnie: sin75^o = sin( 45^o +30^o) = sin45^o*cos30^o + cos45^o *sin30^o podstaw wartośći ( znasz takie... i policz sin75^o podstaw dane do wzorów ,które Ci podałam na Ob i P Drugie zadanie za moment( bo jest ogromna burza i muszę wyłączyć komputer

Proszeeeeee ; (: dziękuję Ci bardzo, byłabym wdzięczna jakbyś mi powiedziała jak zrobic 2, dziekuje

Eta: Już po burzy Rysuję...... cierpliwości...

sylwia gdańsk: u mnie burza byla o 12

sylwia gdańsk: wy pewnie na wschodzie mieszkacie?

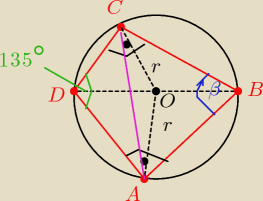
Eta: kąty < A = <B = 90^o −−− bo są kątami wpisanymi opartymi na średnicy suma miar <D + <B = 180^o −−−− to wynika z własności czwosrokata wpisanego w okrąg ( bo suma miar kątów przeciwległych = 180^o więc już zatem wiemy ,że kąt <B = 180^o − 135^o => <B = 45^o kąty: ABC i <AOC −−− to kąty wpisany i środkowy oparte na tym samym łuku AC więc <AOC = 2*<ABC zatem <AOC= 2*45^o => <AOC= 90^o −−− czyli: trójkąt AOC jest prostokątne i równoramienny, bo jego ramiona = r więc IACI = długości przekątnej kwadratu o boku r czyli IACI = r√2 => IACI = 3√2 ( można też z tw. Pitagorasa w tym trójkącie obliczyć IACI bo: IACI² = r² + r² => IACI² = 9 +9 => IACI = √18 to: IACI = 3√2 to wszystko

paula: dzikeuje Ci bardzo mocno

paula: w trapezie ABCD dluzssza podstawa AB ma długosc 8{3} a kat BAD jest rowny 60stopni. Przekatna AC ma dlugosc 6 i zawiera sie w dwusiecznej kata BAD. Oblicz obwod tego trapezu. moglby mi ktos powiedziec jak moge to obliczyc ?

Eta: Witam ....... gimnazjum? czy liceum? to ważne ,bo nie wiem czy znasz f. trygonometryczne? czekam na odp

paula: liceum

paula: obwod ma wyjsc 2√3(6+√7

Eta: Jestem już Rysuję ..... troszkę potrwa, poczekaj!

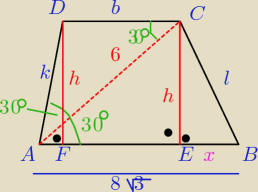
Eta: Rysunek jest:0 więc tak: <BAC= <ACD = 30^o, bo to katy naprzemianległe więc trójkąt ACD jest równoramienny zatem k= b z ΔAEC prostokatnego wyliczamy z funkcji tryg. ^h₆= sin30^o => h= 6* ¹₂ => h= 3 IAEI = 8√3 − x więc z Δ AEC mamy:

	8√3−x
		= cos30o => 8√3 −x = 3√3{2} => x= 5√3
	6

teraz z trójkąta prostokatnego: AFD mamy: ^h_k = sin 60^o => k= 2√3 więc i b= 2√3 pozostaje jeszcze policzyć długość l −−− drugiego ramienia więc z ΔEBC z tw> Pitagorasa: l² = h² + x² => l² = 9 + 75 => l= √84 = 2√21 = 2√3*√7 zatem Ob= 8√3 + 2√3 + 2√3 + 2√3*√7 = Ob= 12√3 + 2√3*√7 = 2√3 ( 6 +√7) Ty powinnaś to zadanie rozwiązywać powodzenia w podobnych zadaniach, myślę ,że już dasz sobie radę

paula: jesteś wielka! najwieksze problemy mam z odczytywaniem tych wszytskich wiaodmosci z rysunku!

Eta: Czy teraz jasne z rysunku?........ rysunek w geometrii ,to podstawa do rozwiazywania takich zadań

mateuzs: Witam 🙂 zadanie wyliczone na piątkę. U mnie nie było burzy. Pozdrawiam Pana i Panią sylwię z gdańska