Mam narysować wykres funkcji cyklometrycznej i wyznaczyć dziedzinę. HelpPlease: Funkcje cyklometryczne − wykres i dziedzina. Proszę o pomoc Mam narysować wykres funkcji cyklometrycznej i wyznaczyć dziedzinę. 2arcsin( 1 − 2x ) Rysunek: http://jpghost.pl/Obraz-3_1354053797/ Chyba coś źle wychodzi. Mógłby ktoś krok po kroku rozpisać przekształcenia jakie powinny być? Dziedzina: −1 ≤ 1 − 2x ≤ 1 −2 ≤ −2x ≤ 0 1 ≥ x ≥ 0 x ∊ <0, 1> Dobrze?

HelpPlease: Pomoże ktoś? Jak po kolei przekształcić wykres arcsinx, aby otrzymać 2arcsin( 1 − 2x )

MQ: 1. Rysujesz arcsin(x) 2. Odbijasz wzgl. osi OY 3. Przesuwasz o 1/2 w stronę dodatnią na osi OX 3. Zacieśniasz o czynnik 2 oś OX 4. Rozciągasz o czynni 2 wzdłuż osi OY

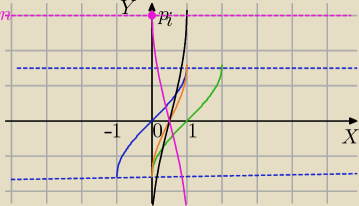
Mila: Dziedzina dobrze. wykres: f(x)=2 arcsin(1−2x)=−2arcsin(2x−1) 1) y=arcsinx translacja o wektor [1;0] niebieski⇒otrzymuje 2)y=arcsin(x−1) zielony zagęśzczam, i otrzymuję 3)y=arcsin(2x−1) pomarańczowy; 4) podwajam wartości y=2arcsin(2x−1) 5) symetria OX i otrzymuję y=−2arcsin(2x−1) Na dole nie zmieścił się.

HelpPlease: czyli 2arcsin(−2x + 1) to jest to samo co 2arcsin −(2x − 1) i się ten "−" wysuwa przed funkcję i mam: −2arcsin(2x − 1)

HelpPlease: I tak bardzo dziękuję za rozpisanie mi tego wszystkiego. Jeszce raz śliczne dzięki

Mila: Arcsinx jest funkcją nieparzystą i to wykorzystałam.