Liczby rzeczywiste Mariusz: Wyznacz wartości parametru m, dla których równanie |x − 1| = m ma dwa pierwiastki różnych znaków. Bardzo proszę o odpowiedź, bo mam wątpliwości czy zdam maturę z matmy rozszerzonej, a to mój cel.

Mati_gg9225535: moze by to obustronnie podnieść do kwadratu ?

Mariusz: Nie mam pojęcia o co w tym chodzi. Może jakby ktoś mi to wytłumaczył to załapałbym.

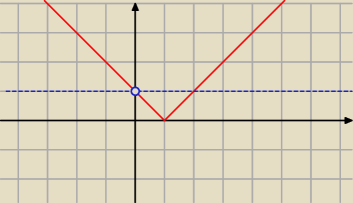
Saizou : można z wykresu i doczytujemy że dla m∊(1:+∞) rozwiązania są różnych znaków

Mariusz: Dzięki bardzo. Jestem głupi. xD

Mariusz: Tylko nie wiem czemu m jest oznaczone jako liczba jeden... Czy po prostu jest to bez różnicy gdzie postawię ten parametr?

Saizou : a przeanalizuj sobie jak się będzie zachowywać wykres przy wybranych "m"

Mariusz: I o co chodzi z tymi różnymi znakami? Proszę o dokładne wyjaśnienie.

ZKS: Można też wykorzystać wzory Viete'a. |x − 1| = m / ² zał m ≥ 0 (x − 1)² = m² x² − 2x + 1 − m² = 0 Pierwiastki mają być różnych znaków więc x₁x₂ < 0 1 − m² < 0 (m − 1)(m + 1) > 0 ⇒ m ∊ (−∞ ; −1) ∪ (1 ; ∞) ale pamiętamy o założeniu że m ≥ 0 ostatecznie dostajemy m ∊ (−∞ ; −1) ∪ (1 ; ∞) ∧ m ≥ 0 ⇒ m ∊ (1 ; ∞).

Mariusz: Rozumiem, że funkcja |x−1| ciągnie się w nieskończoność, a parametr m? To ma znaczyć, że gdziekolwiek bym go postawił funkcja będzie miała rozwiązanie różnych znaków?

Mariusz: Aaaaa... To teraz rozumiem. Bardzo ślicznie dziękuję. Przeanalizuje i utrwale w głowie to zadanie.

Saizou : różne znaki (miejsca zerowa są przeciwnych znaków) zobaczmy że dla m=0 jest tylko jedno rozwiązanie dla m∊(0:1> są dwa rozwiązania dodatnie (bo jest to jakby przesunięcie wykresy o m jednostek w górę albo w dół) dla m>1 mamy 2 rozwiązania przeciwnych znaków

Saizou : panie niewidzialny ZKS ja i tak wolę graficzną metodę

ZKS: Jak kto woli jak kto chce. Chciałem tylko przedstawić inną opcję rozwiązania tego zadania.