badanie zmienności funkcji
Maciek: Cześć!

Słuchajcie, jutro mam kolokwium z matmy ze zmienności funkcji i natrafiłem na przykład,
ktoórego nie mogę zrobić wogoóle. Nawet przy ustaleniu dziedziny mam problem

Zad:
Zbadać zmienność funkcji
| | 1 | |
f(x) = √ |
| //ten pierwiastek jest z całego ułamka |
| | sinx | |
Na początek pytam Was jaka jest dziedzina funkcji i czy funkcja jest parzysta albo nieparzysta

27 lis 20:37
Godzio:
sinx > 0 −− z tego otrzymasz dziedzinę
Funkcja nie jest ani parzysta ani nieparzysta
27 lis 20:38
krystek: a popatrz na wykres sinx
27 lis 20:38
Mila: sinx>0 ( liczba pod pierwiastkiem ≥0 i mianownik ≠0)
x>0+2kπ i x<π+2kπ i k∊C⇔x∊(2kπ;π+2kπ) i k∊C
| | −cosx | |
f '(x)= |
| |
| | 2sinx √sinx | |
| | π | |
f '(x)=0 ⇔cosx=0 i x∊D⇔x= |
| +2kπ tu ma minimum |
| | 2 | |
dalej poradzisz sobie?
funkcja jest okresowa
27 lis 21:32
Maciek: A dlaczego nie liczymy granic lewostronnych dla punktów 0 i π

27 lis 22:10
Maciek: i jakie są granice tej funkcji w +∞ i −∞, żeby znaleźć ewentualnie asymptoty ukośne no i
narysowac wykres
27 lis 22:13
Maciek: Będę bardzo wdzięczny jak ktoś pomoże mi w tym zadaniu i zrobi je całe do końca

27 lis 22:15
Maciek: Proszę o pomoc geniuszy z matmy

27 lis 22:26
krystek: Popatrz na dziedzinę i będziesz wiedział dlaczego nie liczymy lewostronnych
27 lis 22:32
Mila:
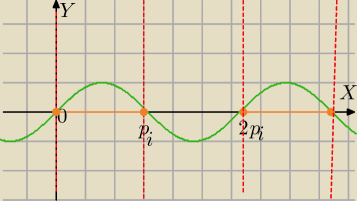
Popatrz na dziedzinę− argumenty na pomarańczowo.
Przepraszam, bo granic powinna być w π
−.
Tam źle mi się wpisało. Prawostronna w π jest bez sensu, bo punkty od π do 2π nie należą do
dziedziny.
powtarzalny wykres mieści się w (0,π)
Spróbuję narysować.
granice w (
∞) i (−
∞) masz uwzględnione , bo funkcja jest okresowa, to wynika z okresowości
sinx.
| | π | | π | |
f( |
| )=U{1}{p{sin |
| )=1 |
| | 2 | | 2 | |
27 lis 22:39
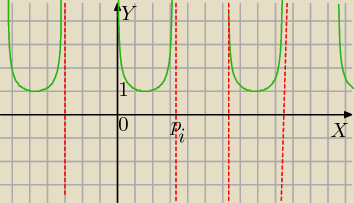
Mila:
27 lis 22:43
Mila: ?
27 lis 22:51
27 lis 23:05
Maciek: hmm... jeszcze nie do końca wszystko rozumiem, ale myślę ciągle nadal

27 lis 23:09
Mila: Jestem, zadaj pytanie.
Edytor bez podglądu powoduje, że inne znaki się wpisze, i trzeba sprawdzać.
27 lis 23:12
Maciek: Czyli granic w +∞ i −∞ nie da sie jednoznacznie określić bo wachają się od (−1;1) ? czy od
(0;1)?
27 lis 23:29
Maciek: a funkcja pochodna nie wynosi czasem:
27 lis 23:31
Maciek: 
27 lis 23:36
Mila: Popatrz na wykres, zbiór wartości <1;∞) dla każdego przedziału dziedziny.
To jest równoważna postać pochodnej, po usunięciu niewymierności z mianownika, czego nie
robiłam, bo wygodniej liczyć miejsce zerowe pochodnej.
27 lis 23:45
Maciek: A jak odowodnić okresowość tej funkcji, że to jest okres π

27 lis 23:49
Mila: | 1 | | 1 | |
| = |
| ; T>0 i T niezależne od x |
| √sin(x) | | √sin(x+T) | |
√sin(x+T)=
√sin(x)⇔
sin(x+T)=sinx co już wystarczy, ale można zapisać
x+T=x+2kπ i k∊C
T=2kπ
28 lis 00:00
Maciek: Ok, wielkie dzięki
28 lis 00:27
 Słuchajcie, jutro mam kolokwium z matmy ze zmienności funkcji i natrafiłem na przykład,
ktoórego nie mogę zrobić wogoóle. Nawet przy ustaleniu dziedziny mam problem
Słuchajcie, jutro mam kolokwium z matmy ze zmienności funkcji i natrafiłem na przykład,
ktoórego nie mogę zrobić wogoóle. Nawet przy ustaleniu dziedziny mam problem  Zad:
Zbadać zmienność funkcji
Zad:
Zbadać zmienność funkcji




 Popatrz na dziedzinę− argumenty na pomarańczowo.
Przepraszam, bo granic powinna być w π−.
Tam źle mi się wpisało. Prawostronna w π jest bez sensu, bo punkty od π do 2π nie należą do
dziedziny.
powtarzalny wykres mieści się w (0,π)
Spróbuję narysować.
granice w (∞) i (−∞) masz uwzględnione , bo funkcja jest okresowa, to wynika z okresowości
sinx.
Popatrz na dziedzinę− argumenty na pomarańczowo.
Przepraszam, bo granic powinna być w π−.
Tam źle mi się wpisało. Prawostronna w π jest bez sensu, bo punkty od π do 2π nie należą do
dziedziny.
powtarzalny wykres mieści się w (0,π)
Spróbuję narysować.
granice w (∞) i (−∞) masz uwzględnione , bo funkcja jest okresowa, to wynika z okresowości
sinx.




