pytanie
adaś:
pytanie.
jak mam −x2 i za iksa daje np. 2 to −22 czy −(2)2 ?
27 lis 17:46
adaś: ?
27 lis 17:50
Beti: to drugie
27 lis 17:52
otka_a: Adaś, a może cały przykład?
Bo jeśli np masz 2x3 − x2
To jak podstawisz to masz 2*23 − 22 = 2*8 − 4 = 16 − 4 = 12
27 lis 17:53
yamaha: tak
27 lis 17:54
Beti: czyli do kwadratu podnosisz tylko liczbę podstawioną za 'x'
27 lis 17:54
adaś:
mam takie coś −x2+4≥0 za x daje 3 , na pewno drugie?
27 lis 17:55
Krzysiek : napisz np w czym masz tak policzyc .
zobacz −22=−4 a takze −(2)2=−4
27 lis 18:05
MQ: −22=−(2)2=−4
ale
(−2)2=(−2)*(−2)=4
27 lis 18:06
adaś:
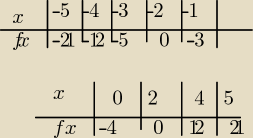
Naszkicuj wykres funkcji f (x) = |x
2 − 4| , a następnie określ liczbę rozwiązań równania |x
2
− 4| = m w zależności od wartości parametru m .
robię sobie tak:
−x
2+4<0
x
2−4≥0
tabelki:
27 lis 18:10
adaś: tabelki powyżej
27 lis 18:10
27 lis 18:11
adaś: dlaczego ?
27 lis 18:11
adaś: ?
27 lis 18:19
adaś: pomoże ktoś ?

27 lis 18:28
MQ: Dla x=−5 powinieneś mieć wartość 21, a nie −21
−4 ==> 12
−3 ==> 5
27 lis 18:33
adaś: dlaczego ? −(−5)2 +4 =−25+4 =−21
27 lis 18:44
adaś: 
27 lis 18:54
Krzysiek : Adas . jesli chodzi o podnoszenie do kwadratu to juz masz wyjasnione.
Teraz masz −x2+4≥0 ,Co chcesz liczyc ze za x podstawiasz 3 . To jest nierownosc kwadratowa i
jeszcze w dodatku slaba bo ≥0 . Tutaj nie robisz tabelki zeby narysowac ten wykres tabelke to
sie robi dla funkcji liniowych i np jak chcesz to dla wykladniczych logarytmicznych
Dla nierownosci kwadratowych musisz okreslic przedzialy dla ktorych jest ona < 0.≤0.>0,≥0
Przeciez nie bedziesz podstawial za x rozne liczby i liczyl zeby zobaczyc czy on spelniaja ta
nierownosc bo CI braknie czasu Tutaj masz −x2+4≥0 Zeby policzyc miejsca zerowe tej funkcji
to zobacz ze masz nierownosc niepelna i mozesz zapisac tak −x2+4=0 ⇒−x2=−4 ⇒x2=4
⇒x=2 bo 22=4 lub x=−2 bo (−2)2=4 lub inaczej (−2)*(−2)=4 Masz wyznaczone miejsca zerowe
czyli x1 =2 i x2=−2 . Teraz do narysowania wykresu brauje CI trzeciego punktu czyli
wierzcholka Wiec albo policzysz wspolrzedne ze wzorow albo zauwzysz ze wykres funkcjiy=
−x2+4 powstaje poprzez przesuniecie wykresu funkcji y=−x2 o 4 jednostki do gory czyli
wierzcholek ma wspolrzedne x=0 i y=4 . Narysuj sobie teraz wykres ramiona w dol bo jest
−x2 i zobacz w jakim przedziale jest ona ≥0 . jak ja narysujesz to zobaczysz ze jest ≥0 w
przedziale <−2,2> . jest to przedzial domkniety bo masz wieksze badz rowne 0
jak by bylo >0 to wtedy by byl przedzial (−2,2)
Chociaz tutaj z eby wyznaczyc przedzial niepotrzebny byl CI wierzcholek zeby to stwierdzic ale
naucz sie rysowac w miare dokladnie parabole zeby np okreslic kiedy funkcja maleje lub rosnie
czyli okreslic monotonicznosc .
Jesli bedzie nierownosc pelna to liczysz standart czyli Δ,x1.x2 wierzcholek i wykres i
okreslasz przedzial
27 lis 18:58
27 lis 19:01
Krzysiek : Myslalem ze chodzi CI o nierownosc ale TYmasz wartosc bezwzgledna . Dla tego podumaj sobie
dobrze nad tym Jesli dobrze przeczytasz to co CI teraz napisalem to nie powinno byc problemu
z rozwiazaniem tego .
Teraz jesli chodzi o ten zapis −(−5)2=−25 dlatego z e (−5)2=25 bo −5*−5 =25 ale masz jeszcze
znak − przed (−5)2 i dlatego jest −25 . Napisz rozwiazanie tego rownania . Tylko napisz bo
TY nie konczysz rozwiazan na forum i potem sa wieksze klopoty .
27 lis 19:06
adaś:
Naszkicuj wykres funkcji f (x) = |x
2 − 4| , a następnie określ liczbę rozwiązań
równania |x
2 − 4| = m w zależności od wartości parametru m .
−x
2+4<0
x
2−4≥0
−x
2+4<0 dla x∊(−2,2)
x
2−4≥0 dla x∊ (−
∞,−2>U<2;
∞ )
i może teraz mam rysować tabelkę i z tabelki na wykres ?
chce zrobić podobnie jak tutaj →
https://matematykaszkolna.pl/strona/2590.html
27 lis 19:12
Krzysiek : DObrze to napisales opuszczajc wartosc bezwzgledna czyli −x+4<0 i x2−4≥0 Teraz napisz w
jakim przedziale −x2+4<0 i w jakim przedziale x2−4≥0 . Pisz rozwiazania na forum to sie
sprawdzi. Wtedy bedzie dla −x2+4<0 to m∊do i dela x2−4≥o m∊do przedzialu
27 lis 19:15
adaś:
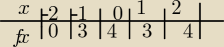
zrobiłem już x∊ ... robię tabelki
−x
2+4<0 dla x∊(−2,2)
27 lis 19:21
adaś: dobrze jest ta tabelka powyżej ?
27 lis 19:21
27 lis 19:23
adaś: 
27 lis 19:31
adaś: proszę o pomoc
27 lis 19:47
Krzysiek : Dla −x2+4<0 jest zle wyznaczony przedzial napisz poprawny
27 lis 19:51
Eta:

czarny wykres y= x
2−4 −−− parabola ramionami do góry W(0,−4) x
1=−2 x
2=2
czerwony wykres y= |x
2−4| odbijasz tę część czarnej paraboli spod osi OX nad oś OX
0 rozwiązań dla m ∊(−
∞,0)
2 rozwiązania dla m=0 v m∊(4,
∞)
3 rozwiązania dla m ....
4 rozwiązania dla m ....
dokończ ....
27 lis 19:56
27 lis 20:02
Eta:
adaś
Tabelki "malujesz" jak zaczynasz się uczyć o funkcji kwadratowej!
Ty zdajesz maturę! więc już powinieneś wiedzieć jak wygląda wykres
np: y= x2−4 , y= −x2+9 , y= ( x−3)2+1 itd....
27 lis 20:10
krystek: Czy Adaś =Adaś z września ? Ponieważ zaczynam wątpić
27 lis 20:12
Eta:
tak

27 lis 20:13
27 lis 20:14
Krzysiek : Adas . Musialem isc do rodzicow ale widze ze juz Eta podala CI rozwiazanie .
Mozesz to jeszcze rozwiazac tak rysujes wykres x2−4≥0 ale ylko ta czesc wykresu co lezy
nad osia Ox a ta czesc pod osia Ox nie rysujesz bo jest wartosc bezwzgledna a wartosc
bezwzgledna nie moze byc ujemna . To samo z wykresem −x2+4<0 rysujesz tylko ta czesc
wykresu co leszy nad osia OX a te czesc co jest pod osia to nie rysujesz z tego wzgledu ze
wartosc bezwzgledna nie moze byc ujemna . Otrzymasz ten sam wykres co narysowala CI ETa
Teraz dokoncz te rozwiazania
27 lis 20:20
adaś: wyobraź sobie że tak robie i nie wychodzi a tabelki będę rysował ETA


!
27 lis 20:23
27 lis 20:24
adaś: to że Eta przerobiłaś może setki takich zadań i znasz niektóre na pamieć może , a może jesteś
nawet po studiach matematycznym to nie znaczy że jak to Ty
27 lis 20:24
adaś: ja*
27 lis 20:25
adaś: mogłaś byś mi skoro widać że jednak można w tabelce sobie to opracować pomóc w zrobieniu tabeli
do zadania →27 lis 18:10 ,?

bo ja już robię kilka i nie wychodzi mi wykres .
27 lis 20:27
adaś: miesza mi się poprostu wszystko z tą wart. bezw. z wykresem, raz zadanie jest inaczej
rozwiązywane a raz zupełnie inaczej
27 lis 20:30
Eta:
Jesteś niegrzeczny i dlatego Ci już nie pomogę

27 lis 20:31
krystek: Adaś idź z postępem , w pierwszej klasie miałeś przekształcanie wykresów
np. y=x2+ 4 rysujesz x2 i przesuwasz w górę o 4 jednostki
27 lis 20:34
krystek: Dodam ,że bardzo .
Eto , i znamy takie przypadki , prawda?
27 lis 20:36
Krzysiek : Przyjmij to z pokora co napisano bo wciaz CI chcemy pomoc a Eta jest mloda i CI wiecej pomoze
niz ja .
Co do tego punktu to ja chyba Cie zamorduje . Chcesz robic tabelki . Prosze robic . TO teraz
narysuj sobie tabelke i wstaw za x=0 do tych funkcji i zobacz ile wyjdzie CI y w 1 i 2
nierownosci Czy czasami nie dwa . czyli bedzie (0,2)
A co do tych powyzej wykresow to sobie je sam zrobilem i wyszly. Tak ze nie ma bata ze nie
wyjdzie
27 lis 20:39
adaś: no ja to rozumiem krystek , chodzi o wartość bezwzględną , to że gdybym sobie y=|x
2+ 4|
rozpisał na dwie możliwości ,
czyli x≥0 i x<0 to otrzymał bym przedziały później , następnie nakładając to na wykres nie
wychodzi wykres jak tutaj
http://img.zadania.info/zad/1/5988781/HzadR3x.gif
27 lis 20:40
27 lis 20:42
adaś: robię to kilka razy i nie chce wyjść
27 lis 20:42
krystek: Co Ty wymyślasz ? jak wygląda wykres x2+4?
27 lis 20:43
adaś: Wybacz Krzysiek oczywiście że (0,2)
27 lis 20:43
adaś: przesunięty o 4 jednostki do góry
27 lis 20:44
krystek: Przecież to zadanie już kiedyś "męczyłeś"
27 lis 20:45
krystek: i tak samo Ix2+4I
27 lis 20:46
adaś: chyba jednak coś innego męczyłem albo mam słabą pamięć
27 lis 20:47
adaś: dobra sam przeanalizuje to jeszcze z tymi wykresami, dzięki Wam za cierpliwość

27 lis 20:48
Krzysiek : Nie |x2+4| bo to by calkiem inny wykres wyszedl tylko y=|x2−4|
jak powstanie wykres takiej funkcji . Rysujesz funkcje y= x2−4. . Narysuj sobie ja . Jest to
parabola y=x2 przesunieta o 4 jednostki w dol . Tak ?.tak . . Miejsca zerowe tej funkcji to
x1=2 i x2=−2 bo x2−4=0 to x2=4 wiec x=2 i x=−2 ..
Ale TY nie masz y=x2−4 ale y=|x2−4| . Wartosc bezwzgledna jest zawsze napisze jeszcze raz
ZAWSZE dodatnia . Teraz ta czesc wykresu y=x2−4 co jest pod osia OX (czyli tam ta funkcja
przyjmuje wartosci ujemne ) a wartosc bezwzgledna y=|x2−4I nie moze byc ujemna to musisz ta
czesc wykresu odbic nad os OX . Otrzymasz w ten sposob wykres y=Ix2−4I ktory narysowala CI
ETA . Prosciej nie umiem wytlumaczyc
27 lis 22:38
krystek: Krzysiek , sądzę ,że Adaś nie czyta tego ze zrozumieniem − już Jemu tłumaczyłeś.
27 lis 22:40
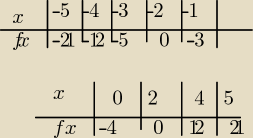 Naszkicuj wykres funkcji f (x) = |x2 − 4| , a następnie określ liczbę rozwiązań równania |x2
− 4| = m w zależności od wartości parametru m .
robię sobie tak:
−x2+4<0
x2−4≥0
tabelki:
Naszkicuj wykres funkcji f (x) = |x2 − 4| , a następnie określ liczbę rozwiązań równania |x2
− 4| = m w zależności od wartości parametru m .
robię sobie tak:
−x2+4<0
x2−4≥0
tabelki:


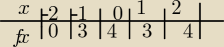 zrobiłem już x∊ ... robię tabelki
−x2+4<0 dla x∊(−2,2)
zrobiłem już x∊ ... robię tabelki
−x2+4<0 dla x∊(−2,2)
 może mi ktoś zrobić →27 lis 2012 19:12 według https://matematykaszkolna.pl/strona/2590.html ?
może mi ktoś zrobić →27 lis 2012 19:12 według https://matematykaszkolna.pl/strona/2590.html ?

 czarny wykres y= x2−4 −−− parabola ramionami do góry W(0,−4) x1=−2 x2=2
czerwony wykres y= |x2−4| odbijasz tę część czarnej paraboli spod osi OX nad oś OX
0 rozwiązań dla m ∊(−∞,0)
2 rozwiązania dla m=0 v m∊(4,∞)
3 rozwiązania dla m ....
4 rozwiązania dla m ....
dokończ ....
czarny wykres y= x2−4 −−− parabola ramionami do góry W(0,−4) x1=−2 x2=2
czerwony wykres y= |x2−4| odbijasz tę część czarnej paraboli spod osi OX nad oś OX
0 rozwiązań dla m ∊(−∞,0)
2 rozwiązania dla m=0 v m∊(4,∞)
3 rozwiązania dla m ....
4 rozwiązania dla m ....
dokończ ....
 czyli jednak tylko Twoim sposobem można to dobrze rozwiązać sądziłem że mogę
podobnie jak tutaj https://matematykaszkolna.pl/strona/2590.html , czyli tabelki itp.
czyli jednak tylko Twoim sposobem można to dobrze rozwiązać sądziłem że mogę
podobnie jak tutaj https://matematykaszkolna.pl/strona/2590.html , czyli tabelki itp.



 !
!



 ! ( czasu na maturze Ci zabraknie
! ( czasu na maturze Ci zabraknie 
 bo ja już robię kilka i nie wychodzi mi wykres .
bo ja już robię kilka i nie wychodzi mi wykres .



