Trójkąt wpisany w trójkąt Niewiemjak: TRÓJKĄT WPISANY W TRÓJKĄT (konstrukcja). Niech będzie dany ( dowolny ) trójkąt ABC i ( dowolnie ustalony ) punkt K ∊ [AB] . W trójkąt ten wpisać trójkąt prostokątny KLM, taki, że ∡K = 90^o, L ∊ [BC], M ∊ [AC], oraz ML || AB. Uzasadnić przebieg konstrukcji.

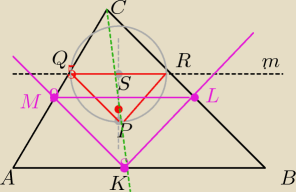
Mila: 1) Kreślę ΔABC 2) konstrukcja prostej m ||AB⇒punkty Q,R 3) symetralna QR ,S środek QR

	1
4) kreślę okrąg ośrodku S i promieniu r=		|QR| otrzymuję punkt P
	2

5) ΔQRP jest prostokątny, bo ∡P jest prosty, jako wpisany oparty na średnicy 6) rysuję półprostą CP^→ otrzymuję punkt K 7) kreślę z punktu K równoległe do PR i PQ) otrzymuję punkty L i M 8)Łączę punkty M i L 9) ΔMKL jest prostokątny i ML||AB Jutro pomyślę nad mniej skomplikowaną konstrukcją. Możesz jeszcze napisać, że ΔMKL iΔQRP są jednokładne .

Niewiemjak: Witaj Mila, « 6) rysuję półprostą CP→ otrzymuję punkt K ». Konstrukcja jest błędna. PUNKT K JEST ZADANY Z GÓRY. W zależności od jego umiejscowienia otrzymujemy ODMIENNE trójkąty prostokątne tzn. o innych kątach ostrych... ( można to sprawdzić np. na Geogebrze ) W zaproponowanej konstrukcji rozumowanie zostało odwrócone: trójkąt prostokątny powstał od prostej paralelnej i wygenerowaniu punktu K...a nie o to chodziło. ( Był to też mój pierwszy odruch...) Dziękuję za zainteresowanie i ... czekam na inną propozycję !

Mila: No to ustalasz punkt K i dopiero wtedy rysujesz półprostą CK^→ Rzeczywiście przeoczyłam "ustalony". Po prostu zmienisz kolejność czynności. Punkt P nie będzie obierany ale .. "Kto zaczął, ten wykonał połowę pracy"− Horacy. Popraw kolejność i będzie dobrze.

Mila: Skąd można bezpiecznie pobrać Geogebrę.

Piotr: np stąd http://www.dobreprogramy.pl/GeoGebra,Program,Windows,24054.html

Piotr: geogebra jest tez w wersji on−line http://www.geogebra.org/webstart/geogebra.html

Mila: Witaj, Piotrze. Dziękuję.

Piotr: Witaj Mila . nie ma sprawy

Mila: 1) ΔABC 2)K∊AB 3) CK^→ 4)QR||AB i QR<AB 5)Okrąg 6) P ; PR i PQ ; ∡RPQ=90⁰ 7)Równoległe dp RP i PQ przechodzące przez K. ⇒L;M ....

Niewiemjak: Witaj, Mila Wygląda na to, że jest ok. Bardzo Ci dziękuję! Do następnego razu na forum... Pozdrawiam, < Niewiemjak >

Mila: Nie "wpadłeś" na inny sposób? Jeśli coś wymyślę, to napiszę.

Mila: Modyfikacja. Możesz ten okrąg narysować inaczej. O(K, r), gdzie r=min(AK,KB) i dalej będziesz chyba wiedział. Będzie przesunięcie do góry. Tak jest prościej.