wielomianową nierówność paulintta: rozwiąż wielomianowy nierówności(x2−2x−15)4(2x+1)≤0

M:

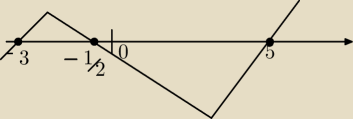
Bo_ra: (x²−2x−15)(2x+1)≤0

	1
2x+1=0 2x=−1 x=−
	2

x²−2x−15=0 Δ=64 √64=8

	2−8
x1=		=−3
	2

	2+8
x2=		=5
	2

x²−2x−15=(x+3)(x−5) (x+3)(x−5)(2x+1)≤0 x∊(−∞,−3]U[−0,5,5]

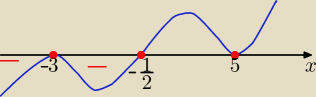NN: Ja tam widzę czwartą potęgę (x²−2x−15)⁴(2x+1)≤0 x=5 v x= −3 −−− pierwiastki czterokrotne oraz x= −1/2 −− pierwiastek jednokrotny x∊(−∞, −1/2]U{5} =============== lub 2/ sposób (x²−2x−15)⁴ ≥0 dla x∊R zeruje się dla x= −3 v x= 5 zatem 2x−1≤0 dla x ≤−1/2 odp: x ∊(−∞, −1/2]U {5}