Geometria Mlody: Napisz równanie stycznych do okręgu : x²+y²−8x−10y+28=0 tworzących z prostą 5x−y+3 kąty równe 45 stopni Pomoże ktoś?

Basia: y = 5x−3 czyli tgα = 5 kąt nachylenia stycznej to α+45 lub α−45

	tgα+tg45		5+1		6		3
tg(α+45) =		=		=		= −
	1−tgα*tg45		1−5*1		−4		2

	tgα−tg45		5−1		4		2
tg(α−45) =		=		=		=
	1+tgα*tg45		1+5*1		6		3

styczne mają więc równania: y = −³₂x+b y = ²₃x+b no i teraz układy równań: y = −³₂x+b x²+y²−8x−10y+28=0 y= ²₃x+b x²+y²−8x−10y+28=0 mają mieć (każdy oddzielnie) jedno rozwiązanie podstawiasz za y; dostaniesz równania kwadratowe i badasz dla jakiej wartości b Δ=0

Mlody: Dziękuję bardzo, mam jeszcze ostatnie pytanie, skąd wziął się tgα = 5? z tego ze wspolczynnik jest 5x?

Basia: tak prosta y = ax+b jest nachylona do osi OX pod kątem α, takim, że tgα=a

Szatą: czemu tgα = 5? wtf : DD

Szatą: nevermind

Basia: napisałam dlaczego o 21:56

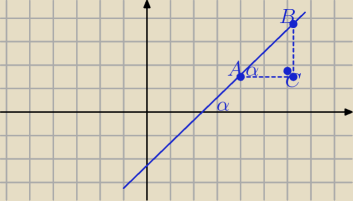
Basia: A(x₁; ax₁+b) B(x₂; ax₂+b) C(x₂, ax₁+b) BC = ax₂+b − ax₁−b = a(x₂−x₁) AD = x₂−x₁

	BC		a(x2−x1)
tgα =		=		= a
	AC		x2−x1

Szatą: tylko zastanawiam się co z tym okręgiem : <