Geometria Kopiko: Znajdź równania prostych zawierających boki trójkąta ABC, jeśli dany jest wierzchołek A(0;2) oraz równania prostych zawierających 2 wysokości H1: x+y−4=0 H2: 2x−y=0 Czy jest ktoś w stanie mi z tym pomóc? Z góry dziękuje

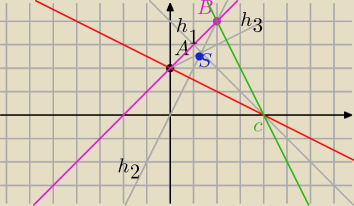
Aga1.: h₁: y=−x+4 h₂: y=2x Bok AC jest prostopadły do wysokości h₂

	1
y=−		x+b
	2

b=2

	1
AC: y=−		x+2
	2

Wysokości przecinają się w punkcie S. x+y=4 2x−y=0 −−−−−−−−−−− 3x=4

	4
x=
	3

y=2x

	8
y=
	3

	4		8
S=(		,		)
	3		3

Prosta zawierająca bok AB jest prostopadła do wysokości h₁ y=x+b b=2 AB: y=x+2 Wierzchołek B to punkt wspólny prostej AB i wysokości h₂ y=x+2 y=2x B(2,4) Wysokość h₃ to prosta AS

	1
Obliczę współczynnik kierunkowy prostej AS a=
	2

Prosta BC przechodzi przez punkt B i jest prostopadła do h₃ y=−2x+b 4=−2*2+b b=8 BC: y=−2x+8