Dowód
Saizou : Kejt pragnę ci przypomnieć o zadaniu
"Dwa boki trójkąta są średnicami dwóch okręgów. Wykaż, że wspólna cięciwa tych okręgów jest
wysokością trójkąta"
25 lis 20:20
Saizou : obywatelka Kejt wzywana
25 lis 20:42
Kejt: obecna! przepraszam, nie wymyśliłam jeszcze niczego czym mogłabym się pochwalić.

25 lis 20:43
Saizou :
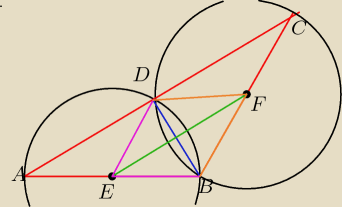
niech rysunek będzie podpowiedzią
25 lis 20:52
Kejt: rysunek to ja już mam, ale dziękuję.
25 lis 20:53
Saizou : zauważ że trójkąty ABC i EBF są podobne i czym są odcinki EFi BD

25 lis 20:57
Kejt: przekątnymi rombu..
25 lis 20:58
Saizou : nie rombu a ....
25 lis 20:59
Kejt: czworokąta

równoległoboku?
25 lis 21:00
Saizou : pierwsza litera to d _
25 lis 21:02
think: cóż jedyna myśl która mi się kołacze, to taka, że ponieważ środki leżą na jednej prostej
(genialne, zważywszy na to, że dowolne dwa punkty są współliniowe...) ale w przypadku okręgów,
cięciwa jest symetralną odcina EF. Odcinek EF jest równoległy do AC ( z tw. talesa stanowi
połowę EF) więc prosta prostopadła do AC jest prostopadła do EF a jeśli jest prostopadła to
jest wysokością tego trójkąta. Ale geometria to nie moja mocna strona, więc mogę się mylić.
25 lis 21:03
Eta:
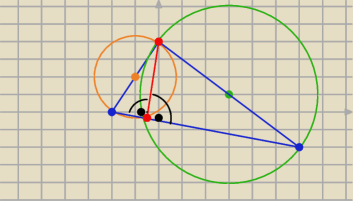
25 lis 21:04
Saizou : think to jest zadanie dla Kejt
25 lis 21:04
think: sorka myślałam, że to Twoje zadania, w którym Kejt obiecała Ci pomóc...
25 lis 21:05
Eta:
Hej
think 
Kopę lat nie gadałaś ze mną


(rudy .... pamiętam

25 lis 21:07
think:  Witaj Kochana Etuniu
Witaj Kochana Etuniu, trochę mnie nie było

ale jak jestem to jestem i przenigdy
o Tobie nie zapomniałam!
25 lis 21:08
Eta:


25 lis 21:12
Kejt: deltoid!
25 lis 21:12
Saizou : 
, zatem pod jakim kątem się przecinają
25 lis 21:13
Kejt: prostym!
25 lis 21:14
Saizou : wiec już jest z górki, czekam na przedstawienie całego dowodu
25 lis 21:16
think: 
moja kić jest pręgowany szaro−czarny

25 lis 21:19
licealista: ja ten dowód miałem na konkursie w sobotę

25 lis 21:26
think: no fakt, zadanie zalatywało na coś konkursowego

tym bardziej jestem z siebie dumna

bo mam
szczególne braki z geometrii.
25 lis 21:28
Saizou : licealisto masz rację jest to zadanie konkursowe z "Supermatematyka", który miał miejsce w
sobotę
25 lis 21:31
Vax:
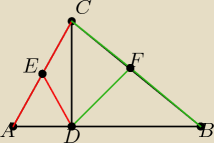
Niech D będzie spodkiem wysokości opuszczonej z C, E środkiem |AC| , F środkiem |BC|. Wystarczy
zauważyć, że skoro trójkąty ADC oraz BDC są prostokątne, to środkami okręgów opisanych na nich
są odpowiednio punkty E,F. Tak więc okrąg o środku E przechodzi więc przez punkty C, D oraz
tak samo okrąg o środku F przechodzi przez C i D, więc wspólną ich cięciwą jest CD − wysokość
poprowadzona z wierzchołka C.
25 lis 21:42
Saizou : Vax jak zawsze oryginalnie

25 lis 21:46

 niech rysunek będzie podpowiedzią
niech rysunek będzie podpowiedzią

 równoległoboku?
równoległoboku?

 Kopę lat nie gadałaś ze mną
Kopę lat nie gadałaś ze mną 
 (rudy .... pamiętam
(rudy .... pamiętam
 Witaj Kochana Etuniu, trochę mnie nie było
Witaj Kochana Etuniu, trochę mnie nie było ale jak jestem to jestem i przenigdy
o Tobie nie zapomniałam!
ale jak jestem to jestem i przenigdy
o Tobie nie zapomniałam!


 , zatem pod jakim kątem się przecinają
, zatem pod jakim kątem się przecinają
 moja kić jest pręgowany szaro−czarny
moja kić jest pręgowany szaro−czarny

 tym bardziej jestem z siebie dumna
tym bardziej jestem z siebie dumna  bo mam
szczególne braki z geometrii.
bo mam
szczególne braki z geometrii.
 Niech D będzie spodkiem wysokości opuszczonej z C, E środkiem |AC| , F środkiem |BC|. Wystarczy
zauważyć, że skoro trójkąty ADC oraz BDC są prostokątne, to środkami okręgów opisanych na nich
są odpowiednio punkty E,F. Tak więc okrąg o środku E przechodzi więc przez punkty C, D oraz
tak samo okrąg o środku F przechodzi przez C i D, więc wspólną ich cięciwą jest CD − wysokość
poprowadzona z wierzchołka C.
Niech D będzie spodkiem wysokości opuszczonej z C, E środkiem |AC| , F środkiem |BC|. Wystarczy
zauważyć, że skoro trójkąty ADC oraz BDC są prostokątne, to środkami okręgów opisanych na nich
są odpowiednio punkty E,F. Tak więc okrąg o środku E przechodzi więc przez punkty C, D oraz
tak samo okrąg o środku F przechodzi przez C i D, więc wspólną ich cięciwą jest CD − wysokość
poprowadzona z wierzchołka C.
