Twierdzenie cosinusów Isus:

	a2 + b2
Korzystając ze wzoru na twierdzenie cosinusów wykaż, że		= 12 ,
	d12 + d22

gdzie a i b są długościami boków równoległoboku oraz d1 i d2 są długościami jego przekątnych. Jakby ktoś mógł to rozpisać byłbym wdzięczny.

Isus: Umie ktoś to zrobić ?

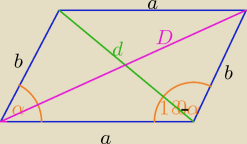Eta: cos(180^o−α)= −cosα z tw. cosinusów d²=a²+b²−2ab*cosα i D²=a²+b²−2ab*cos(180^o−α) D²=a²+b²+2ab*cosα −−−−−−−−−−−−−−−−−−− d²+D²= 2a²+2b² d²+D²= 2(a²+b²) to:

a2+b2		1
	=
d2+D2		2

c.n.u