Ciągłość funkcji ???: Zbadać ciągłość funkcji zadanych za pomocą wzorów: 2 gdy x=0 lub x=+−2 f(x)= 4−x² gdy 0<|x|<2 4 gdy |x|>2 Ja to zrobiłem tak: wziąłem pod uwagę znaki czyli < − lewo i > − prawo i zrobiłem to tak: lim lim x−>0− f(x}= x−>0− (4−x²) = 4− 0²=4 lim lim x−>0+ f(x) x−>0+ 4 = 4 lim lim x−>2− f(x) = x−>2− (4−x²) 4−2² = 4−4=0 lim lim x−>2+ f(x) x−>2+ 4 =4 Odpowiedź jest {−2,0,2} nie wiem dlaczego... A wie ktoś jak zrobić to: −1 gdy x<0 f(x) = sgn x:= 0 gdy x=0 1 gdy x>0 co to jest sgn. Bardzo proszę o rozwiązanie. Rozwiązanie tutaj to wszystko oprócz zera jak to mam rozumieć?

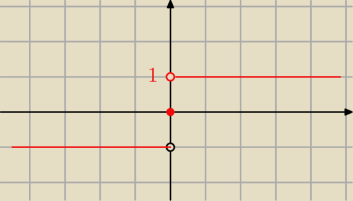
Aga1.: Masz definicję funkcji f(x). signum w skrócie sgnx inaczej znak x. A oto jej wykres.

???: Dobrze ale prosiłbym po kolei> Proszę o wyjaśnienie 1...

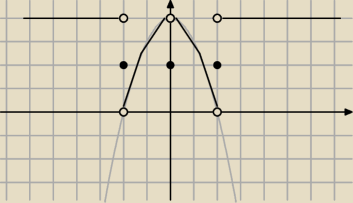
Aga1.: Wykres pierwszej funkcji

Aga1.: I teraz powie4dz, kiedy funkcja jest ciągła w np. punkcie 2. Liczysz granice jednostronne. lim x→2⁻f(x)=2 limx→2⁺f(x)=4 granice jednostronne nie są równe, więc funkcja nie m granicy w punkcie 2 i dalej nie ma co liczyć i odp. Funkcja nie jest ciągła w 2.

Aga1.: limx→0⁺f(x)=limx→0⁻f(x)=4 Istnieje granica w x=0 i wynosi 4, ale f(0)=2 i nie istnieje granica, bo granica nie równa się wartości funkcji w 0. Aby funkcja była ciągła w punkcie to wszystkie wyniki muszą być takie same.

Aga1.: Dopisz ostatnie obliczenia limx→−2⁻f(x) i dalej

???: ale tam w pierwszym przykładzie pisze że jest ciągła w −2,0 i 2 chyba kurde już nic nie czaje jest ciągła dla x należącego do rzeczywistych {−2,0,2} A w tym drugim co mam liczyć?

Aga1.: A może jest tak Funkcja jest ciągła dla x∊R−{−2,0,2} ?

???: X∊R{−2,0,2} Proszę o wyjaśnienie