parabola Krzychu: Wyznacz te wartosci parametru k dla ktorych kazda liczba x∊<−2;3) jest rozwiazaniem nierownosci (x+k−5)(2k+1−x)>0 x₁=5−k x₂=2k+1 Tworze układ równań: 5−k≥−2 2k+1<3 Albo odwrotnie: 5−k<3 2k+1≥−2 I dlaczego to jest źle?

AC: Pierwszy układ zachodzi, gdy 5−k < 2k+1 ⇒ k>4/3 drugi odwrotnie k<4/3 Jeśli to uwzględnisz to o ile dobrze policzyłem to w pierwszym nie ma rozwiązań, a z drugiego k∊<−1/2; 4/3)

AC: a po za tym twoje nierówności mają złe znaki powinny być w drugą stronę.

AC: Jak to porządnie przeliczysz to otrzymasz: k∊(−∞; −1,5 > ∪ < 7; ∞)

Krzychu: ale właśnie nie czaje tego, dlaczego inne znaki

Krzychu: ?

pigor: ..., a masz może do tego odpowiedź, bo mnie "wychodzi" −³₂ ≤ k < 0 i nie wiem , czy warto pisać dlaczego tak ...

Krzychu: odpowiedz jest właśnie taka jaką podał AC.

pigor: ... no to kurcze muszę jeszcze pomyśleć ....

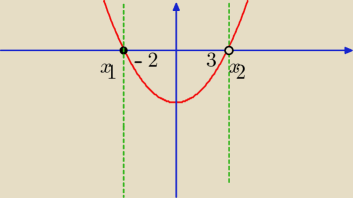
ZKS: (x + k − 5)(x − 2k − 1) < 0 Więc x₁ ≤ −2 ∧ x₂ > 3 (ponieważ nasze x muszą być w przedziale x ∊ [−2 ; 3) ) −k + 5 ≤ −2 ∧ 2k + 1 > 3 ∧ 2k + 1 > −k + 5

	4
k ≥ 7 ∧ k > 1 ∧ k >		⇒ k ∊ [7 ; ∞)
	3

lub −k + 5 > 3 ∧ 2k + 1 ≤ −2 ∧ −k + 5 > 2k + 1

	3		4		3
k < 2 ∧ k ≤ −		∧ k <		⇒ k ∊ (−∞ ; −		]
	2		3		2

	3
k ∊ (−∞ ; −		] ∪ [7 ; ∞)
	2

ZKS: Jak nie będziesz nadal rozumiał napisz postaram się wyjaśnić jeszcze.

Krzychu: Własnie ja nie rozumiem tego, że skoro rozwiązaniem nierówności jest przedział <−2;3) , a pytają w Twojej wersji gdzie parabola przyjmuje wartości ujemne, to dla mnie, te właśnie iksy z tego przedziału, mają się znajdować pomiędzy tymi −2 i 3. Czyli daje założenia, że: k − 5≥−2 , czyli te rozwiązanie jest większe równe od x=−2 2k+1<3 czyli że te rozwiązanie jest mniejsze od x=3 i tak by było dla mnie . Co tutaj źle rozumiem?

pigor: ... ja też mam pewne wątpliwości dlatego podaj może podręcznik, w którym jest to zadanie

Krzychu: kielbasa czesc 1

ZKS: Ale te −2 i 3 to tak jakby pierwiastki Twojej funkcji kwadratowej czyli −k + 5 = −2 i 2k + 1 = 3 więc jeżeli pierwiastki będą większe od −2 i mniejsze od 3 to rozwiązaniem nierówności będą liczby większe od −2 ale mniejsze od 3 więc iksy nie znajdą się w przedziale [−2 ; 3) tylko na przykład (−1 ; 2) lub (0 ; 1). Ale jeżeli pierwiastki będą mniejsze od −2 i większe od 3 to Twój przedział będzie wyglądał na przykład tak (−4 ; 5) lub (−8 ; 10) więc x które są z przedziału [−2 ; 3) znajdą się tam. Rozumiesz o co chodzi?

ZKS: 5 − k < x < 2k + 1 −2 ≤ x < 3 5 − k ≤ −2 < 3 < 2k + 1 5 − k < 2k + 1 lub 2k + 1 < x < 5 − k −2 ≤ x < 3 2k + 1 ≤ 2 < 3 < 5 − k 2k + 1 < 5 − k

pigor: ... dzięki . ...

Krzychu: oni dają nierówność ostrą <−2 w obydwu przypadkach, i ≥3, czego już totalnie nie ogarniam... Teraz skupiam się nad tym od ZKS, jak załapie dam znać

Krzychu: ok wiem o co chodzi już mniej więcej, ale głupie jest to zadanie muszę przyznać. Co o tych nierównościach sądzicie?

ZKS: Jeżeli będziemy mieli pierwiastki równe −2 i 3 to funkcja nasza będzie miała postać (x + 2)(x − 3) < 0 ⇒ x ∊ (−2 ; 3) więc przy −2 powinien być zwykły zwrot nierówności a przy 3 powinien być ostry bo dla x ∊ [−2 ; 3) mamy mieć spełnioną nierówność zawsze ale dla pierwiastka równego −2 to nie zajdzie.

ZKS: Proszę pigor.

Krzychu: więc to co oni napisali z tym 5−k≥3 i 2k+1<−2 jest ok?

ZKS: Tak. Na początku się pomyliłem chyba już śpiący jestem. Ale mam nadzieję że wszystko już teraz jasno wytłumaczyłem?

pigor: ... ja też już załapałem, ale wolę taki układ nierówności spełniający warunki zadania: f(−2) >0 i f(3) ≥0 ⇔ .... ⇔ k∊(−∞ ;−³₂) U (7 ;+∞) −−−−−−−−−−−−−−−−−−−−−−−−−− oba przedziały otwarte, bo k= −³₂ , k=7 nie spełniają warunków zadania , np. dla k=7 , wartość x=−2 nie spełnia danej nierówności...

pigor: ... bo jest nierównościa ostrą .

ZKS:

Krzychu: dobra czaje dzięki

ZKS: Na zdrowie.