funkcja
Ritka: Funkcja f(x)=x2+bx+c przyjmuje wartości ujemne tylko dla x∊ (0;3). Wskaż jej wzór
A. f(x)=x2−9 B. f(x)=x2−3x C. f(x)=x2−3x−1 D. f(x)=−x2+3x
24 lis 20:16
24 lis 20:24
Eta:
a=1 i x1=0 x2=3
to: f(x)=x(x−3)= x2−3x
odp: ........
24 lis 20:28
drah: ale ten przedzial nie jest domkniety, wiec czemu bieżecie 0 i 3?
16 gru 12:22
Piotr:
bo 0 i 3 to miejca zerowe.
16 gru 12:24
drah: ale przedzial tych miejsc nie jest <0;3> tylko (0;3) chyba ze sie myle
16 gru 12:26
drah: i czy jakieś znaczenie ma ze przyjmuje wartości ujemne?Czy jakby bylo wartości dodatnie coś by
to zmieniało?
16 gru 12:26
Piotr:
dla x = 0 y =0
dla x = 3 y = 0
to dla 0 i 3 wartosci sa ujemne czy dodatnie ?
ma znaczenie czy ujemne czy dodatnie.
16 gru 12:35
Aga1.:
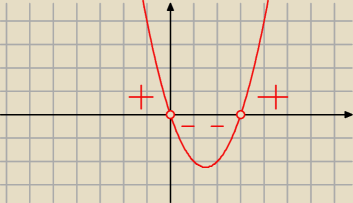
16 gru 12:46
Krzysiek : Oczywiscie ze ma to ogromne znaczenie ze funkcja przyjmuje wartosci ujemne na tym przedziale a
nie dodatnie Jakby bylo ze przyjmuje wartosci dodatnie to zmienilby sie przedzial bylo by
wtedy x∊(−∞,0)U(3,∞) Narysuj sobie ta funkcje i zobczysz ze tak jest naprawde . Wspolczynnik
przy x jest dodatni
wiec raniona paraboli w gore
A teraz dla treningu prosze napisz w jakim przedziale funkcja f(x)=−x2−3x przyjmuje wartosci
ujemne i a jakim dodatnie . Zobacz ze tu masz ramiona paraboli w dol . NO ale napisz i
wyciagnij z tych dwoch przykladow odpowiednie wnioski .Tez napisz jakie wnioski CI sie
nasunely. Czekam na odpowiedz
16 gru 13:13
Krzysiek : Brak odzewu.
16 gru 16:41
dipsy111: kΔrwα ! powalone zadania
14 kwi 16:04
