oblicz objętość bryły lora: Oblicz objętość bryły w R³ ograniczonej powierzchniami x²+y²+z²=4, x²+y²=3x. wytłumaczy to ktoś prostym językiem jak należy takie zadanie zrobić rozwiązując je?

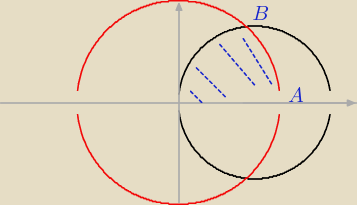
Krzysiek: rzutujesz tą bryłę na płaszczyznę OXY, otrzymując te okręgi i wyznaczasz granice całkowania dla 'x' i 'y' dla tego obszaru niebieskiego (na końcu wynik mnożysz przez dwa, bo ten sam obszar jest pod osią X ) granice całkowania dla 'z' są znane: z∊[−√4−x² −y² ,√4−x² −y² ] Zacząłem Sam liczyć, ale albo się pomyliłem, albo ciężko będzie to liczyć korzystając z przejścia na współrzędne biegunowe...Więc chyba zostaje normalne liczenie tych całek.

lora: a dla x,y jakie bedą granice całkowania?

Krzysiek: A to Sama spróbuj znaleźć np. odczytując z rysunku ,należy znaleźć współrzędne punktów A i B.

lora: wspólrzędne A=(0,2) a B to nie wiem

lora: przepraszam A=(2,0)

Krzysiek: B wyliczysz porównując dwie krzywe: x² +y² =4 x² +y² =3x

lora: aha czyli za z=0 to wtedy sa te dwa równania. z tego x=⁴₃ y²=4−¹⁶₉ czyli y²=²⁰₉ y=^2√5₃ lub y=−^2√5₃

Krzysiek: tak, przyjmij, y>0 a potem wynik pomnożysz przez 2.

lora: czyli granice całkowania dla x to od 0 do 2 a dla y od 0 do ^2√5₃?

lora: a jaka będzie funkcja podcałkowa?

Krzysiek: jeżeli liczysz całkę potrójną to nie ma funkcji podcałkowej tzn ∫∫∫_A dxdydz =objętość bryły ograniczonej obszarem A. z tymi granicami całkowania to źle.. przecież z tych ograniczeń wychodziłoby, że mamy prostokąt. dla x∊[0,4/3] ,y∊[0,√3x−x² ] dla x∊[4/3,2] ,y∊[0,√4−x²]

lora: to nie wiem już jak ma być