.
asdf:
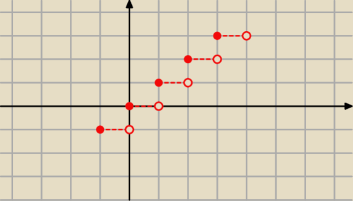
funkcja entier
f(x) = E(x
2) − to mam narysować, prosiłbym o wskazówki, a nie gotowce.
E(x) =
dla x∊ <−1,0) = −1
dla x∊ <0,1) = 0
dla x∊ <1,2) = 1
dla x∊ <2,3) = 2
dla x∊ <3,4) = 3
E(x
2):
dla x
2∊ <−1,0) = −1
dla x
2∊ <0,1) = 0
dla x
2∊ <1,2) = 1
dla x
2∊ <2,3) = 2
dla x
2∊ <3,4) = 3
Graficznie jest przedstawiony tylko wykres funkcji f(x) = E(x)
22 lis 22:59
Artur_z_miasta_Neptuna:
pytanie −−− x
2 ∊ <−1;0)

22 lis 23:00
asdf: czyli DF = <;∞)?
22 lis 23:01
Basia:
rozpisane dobrze pod warunkiem, że znajdziesz jakieś x
2∊<−1;0)

22 lis 23:02
Artur_z_miasta_Neptuna:
wskazówka ... spójrz na to jaka funkcja ma części wspólne ze wszystkimi

początkami kolejnych
przedziałów funkcji
tak samo będzie w przypadku E(x
2) tylko oczywiście inną funkcję bierzesz

22 lis 23:03
Artur_z_miasta_Neptuna:
mam nadzieję, że wiesz o co mi chodzi
22 lis 23:03
Basia:
[x2] = 0 ⇔ x2∊<0;1) ⇔ x∊(−1;1)
[x2] = 1 ⇔ x2∊<1;2) ⇔ x∊(−√2;−1>∪<1;√2)
[x2] = 2 ⇔ x2∊<2;3) ⇔ x∊(−√3;−√2>∪<√2;√3)
i tak dalej
22 lis 23:04
asdf: nie wiem o co chodzi

22 lis 23:05
asdf: a mozesz mi to rozpisac bardziej z kad sie wzielo:
x2e<0;1)⇔ xe(−1;1)?
22 lis 23:07
Basia: na miłość boską asdf; idź spać
x2∊<0;1) ⇔ 0 ≤ x2 < 1 ⇔ x∊R ∧ x2<1 ⇔ x∊R ∧ x2−1 < 0
parabolę sobie narysuj
22 lis 23:09
asdf: x2 = 0 dla przedzialu x2∊<0;1)⇒ 0≤x2<1→ x2 ≥ 0 (czyli wszystkie liczby naturalne) oraz
x2 − 1 < 1 czyli przedział (−1;1)..A jak zero ma się do tego? [x2] = 0?
22 lis 23:16
Basia:
[02] = [0] = 0
poza tym 0∊(−1;1)
22 lis 23:17
asdf:
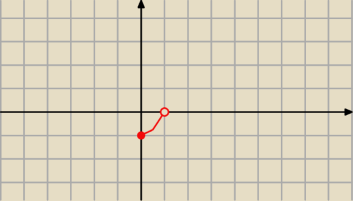
tak będzie wyglądala część E(x
2) dla x∊<0;1)?
22 lis 23:23
asdf: nie rozumiem tego kompletnie

22 lis 23:25
22 lis 23:26
Artur_z_miasta_Neptuna:
niee
22 lis 23:26
Artur_z_miasta_Neptuna:
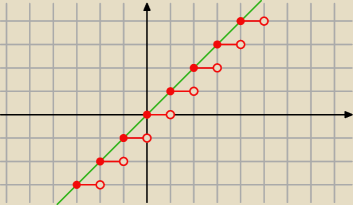
zielona prosta (y=x) to prosta 'pomocnicza'
22 lis 23:28
asdf: wejdzie ktos?
22 lis 23:28
Basia:
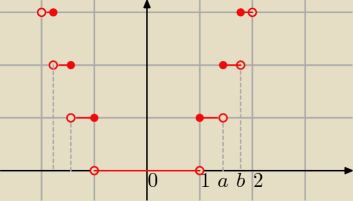
ależ nie; a=
√2 b=
√3
i symetria względem OY
[x
2] = 0 dla x∊(−1;1)
[x
2] = 1 dla x∊(−
√2; −1>∪<1;
√2)
22 lis 23:28
Artur_z_miasta_Neptuna:
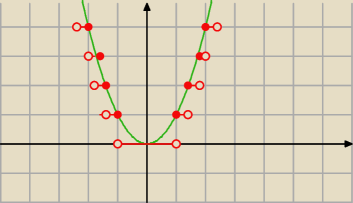
to było E(x)
analogicznie E(x
2) będzie miało postać:
(zielona krzywa y=x
2 to krzywa pomocnicza)
22 lis 23:30
Artur z miasta Neptuna:
Cholera ... nie ... To co myslales to nie hylo dobrze ... Prawidlowe przedzialy zaznavzasz na
osi OX
22 lis 23:58
asdf: ?
23 lis 00:05
asdf:
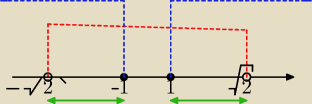 x2 ≥ 1 ⇒ x ∊ (−∞;−1>u<1;∞)
x2 < 2 ⇒ x ∊ (−√2;√2)
x2 ≥ 1 ⇒ x ∊ (−∞;−1>u<1;∞)
x2 < 2 ⇒ x ∊ (−√2;√2)
o to chodzi?
y = 1 dla x ∊(−
√2;−1>u<1;
√2)
23 lis 00:16
asdf: ?
23 lis 00:21
asdf: Mi się wydaje, że to się powinno liczyć z wartości bezwzględnej.
23 lis 00:22
Basia: o to chodzi od samego początku

tylko porządniej to można zapisać
[x
2] = 1 ⇔ 1 ≤ x
2 < 2 ⇔ [ x
2≥1 ∧ x
2<2 ] ⇔ [ x
2−1≥0 ∧ x
2−2<0 ] ⇔
x∊(−
∞;−1>∪<1;+
∞) ∧ x∊(−
√2;
√2) ⇔
x∊[(−
∞;−1>∪<1;+
∞)]∩(−
√2;
√2) ⇔ x∊(−
√2;−1>∪<1;
√2)
23 lis 00:24
Basia:
no przecież to wszystko jedno
1≤x2<2 ⇔ 1≤|x|<√2
23 lis 00:25
asdf: @Basia
No ok, tylko jak pisalem wyzej − nie mialem tego wczesniej, a jak mialem to nie na takim
poziomie (wiem, ze wydaje sie to smieszne, ale nauczyciele tak robią w szkole średniej − malo
wartosci bezwzglednej na maturze to i malo zadan...). Jakos probuje do tego wszystkiego dojsc
i sie połapać w tym

23 lis 00:27
asdf: f(x) = E(log2x)
całkowite będą dla x ∊{1,2,4,8,16,...}
E(x) = 0 dla x∊<0;2)
E(x) = 1 dla x ∊<2;4)
E(x) = 2 dla x ∊<4;8)
E(x) = 4 dla x ∊<8;16)
....
23 lis 00:36
Basia: bardzo dobrze


23 lis 00:38
asdf: Tylko chyba mam źle
E(x) = 3 dla x ∊<8;16)
23 lis 00:39
asdf:
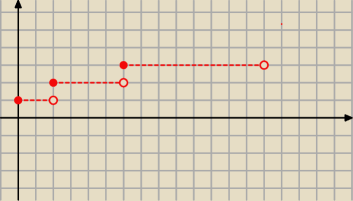
tak to będzie wyglądało?
23 lis 00:41
Basia:
można sobie uogólnić
E(log2x)= 0 ⇔ x∊(0;2)
przecież z definicji logarytmu x>0
k∊Z+
E(log2x) = k ⇔ x∊<2k; 2k+1)
23 lis 00:42
Basia: tak tylko dla x=0 E(log2x) nie istnieje, bo log20 nie istieje
(przedtem to przeoczyłam)
23 lis 00:43
asdf: Ok

Dzięki za wskazówkę

Logarytmów też nie miałem, dlatego teraz mam takie kombo: wartość
bezwzględna + logarytmy...
23 lis 00:43
Basia: oj nie o jednostkę za wysoko na osi OY
narysuję Ci
23 lis 00:44
asdf: Aha, to dla innych funkcji (kwadratowej, itd) miałbym dla zera, ale logarytm z definicji mówi,
| | 1 | |
że to liczby > 0, czyli nie mogę przyjąć, że jak jest |
| to log2x, x ∊(0,1) = log20, |
| | 2 | |
coś w tym stylu?
23 lis 00:45
asdf: Tak, o jednostkę za wysoko, nie trzeba − już będę mieć to na papirusie idealnie.
23 lis 00:46
asdf: z logarytmem jest tak samo jak z funkcją kwadratową, nie znajdę całości z funkcji kwadratowej
dla liczb ujemnych?, tylko w logarytmach jest tylko dla dodatnich.
23 lis 00:47
Basia:
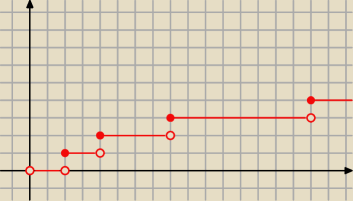
23 lis 00:48
Basia: normalna dziedzina
E(f(x)) istnieje tam i tylko tam gdzie istnieje f(x)
E(x2) x∊R
E(logax) x>0
E(√x) x≥0
E(1x) x∊R\{0}
i tak dalej
23 lis 00:51
Artur_z_miasta_Neptuna:
Basiu ... niezgodzę się co do wykresu
log
ax dla x∊<1;a) E(log
ax) = 0

a E(log
ax) przyjmuje ujemne ... i to straszliwie krótkie przedziały będą
23 lis 00:53
asdf: dziękuję, a jak wyznaczyć tutaj dziedzinę? Proszę tylko o wskazówki
f(x) = log7[log1/2(x2 − 7x + 12) + 1]
23 lis 00:53
Basia: oczywiście masz rację, coś mi się pokręciło; chyba pora spać
E(log2x) = 0 ⇔ x∊<1;2)
tego przedziału (0,1) w ogóle chyba nie da się rozrysować
rozpisać można; nawet łatwo
23 lis 00:55
Basia:
1.
x2−7x+12>0
2.
log1/2(x2−7x+12)+1 > 0
log1/2(x2−7x+12) > −1
x2−7x+12 < (12)−1
x2−7x+12 < 2
23 lis 00:57
asdf: x2 − 7x + 12 > 0
x2 − 7x + 10 < 0
częśc wspólna?
23 lis 01:00
Basia: oczywiście

oba warunki muszą być spełnione
23 lis 01:01
asdf: f(x) =
√log(x2 − 5x + 6) + 1
x
2 − 5x + 6 > 0
log(x
2 − 5x + 6) + 1 ≥ 0
log(x
2 − 5x + 6) ≥ −1
i część wspólna pierwszego z ostatnim tak?
23 lis 01:04
Basia: tak

23 lis 01:06
asdf: log = log
10
−1 = log
10x
10
−1 = x
i jak są te same podstawy logarytmu to można je opuscić?
23 lis 01:09
asdf: log = log10
23 lis 01:09
asdf: f(x) =
√log1/2(x + 1) + 3 +
√x2 − 2x
x + 1 > 0
log
1/2(x+1) + 3 > 0
log
1/2(x + 1) > −3
log
1/2x = −3
x = 8
x + 1 < 8 (zmieniam znak bo log
ab, gdzie a ∊(0;1)
x < 7
x
2 − 2x ≥ 0
i mam:
x + 1 > 0
x < 7
x
2 − 2x ≥ 0
−−−−−−−−−−−
x > −1
x < 7
x(x − 2)≥ 0, x∊(−
∞;0>u<2;
∞)
czyli część wspólna to:
x∊ (−
∞;1)u<2;7)
tak?
23 lis 01:17
asdf: ?
23 lis 01:30
Basia: niezupełnie
1.
x+1 > 0 ⇔ x>−1 ⇔ x∊(−1;+∞)
2.
log1/2(x+1)+3 ≥ 0
log1/2(x+1) ≥ −3
x+1 ≤ (12)−3
x+1 ≤ 8
x ≤ 7
x∊(−∞;7>
3.
x2−2x ≥ 0
x(x−2)≥ 0
x∊(−∞;0>∪<2;+∞)
czyli
x∊(−1;+∞)∩(−∞;7>∩[(−∞;0>∪<2;+∞)] = (−1;0>∪<2;7>
23 lis 01:31
asdf: Ok, dzięki.
| 1 | | 9 | |
| log(2x + 7) + log√7x + 5 = 1 + log |
| |
| 2 | | 2 | |
| | 2x + 7 | | 90 | |
log( |
| )1/2 =log( |
| ) |
| | 7x + 5 | | 2 | |
| | 2x + 7 | |
( |
| )1/2 ={90}{2} |
| | 7x + 5 | |
i na krzyż?
23 lis 01:39
asdf: 
23 lis 02:05
Basia:
dlaczego po lewej dzielisz ?
logx+logy = log(x*y)
log[(2x+7)1/2*(7x+5)1/2 = log45
(2x+7)(7x+5) = 452
chyba, że tam był "−"
23 lis 02:20
asdf: tak, był tam minus

23 lis 02:23
Basia: no to w porządku; oczywiście "na krzyż"

| | 8100 | |
albo bardziej rozsądnie: |
| = 2025 |
| | 4 | |
2x+7 = 2025(7x+5)
tak czy owak okropieństwo jakieś

23 lis 02:29
asdf: nom

dziękuję Ci bardzo za pomoc, trzeba iść spać, dobranoc.
23 lis 02:40
Basia: Dobranoc

23 lis 02:43
 funkcja entier
f(x) = E(x2) − to mam narysować, prosiłbym o wskazówki, a nie gotowce.
E(x) =
dla x∊ <−1,0) = −1
dla x∊ <0,1) = 0
dla x∊ <1,2) = 1
dla x∊ <2,3) = 2
dla x∊ <3,4) = 3
E(x2):
dla x2∊ <−1,0) = −1
dla x2∊ <0,1) = 0
dla x2∊ <1,2) = 1
dla x2∊ <2,3) = 2
dla x2∊ <3,4) = 3
Graficznie jest przedstawiony tylko wykres funkcji f(x) = E(x)
funkcja entier
f(x) = E(x2) − to mam narysować, prosiłbym o wskazówki, a nie gotowce.
E(x) =
dla x∊ <−1,0) = −1
dla x∊ <0,1) = 0
dla x∊ <1,2) = 1
dla x∊ <2,3) = 2
dla x∊ <3,4) = 3
E(x2):
dla x2∊ <−1,0) = −1
dla x2∊ <0,1) = 0
dla x2∊ <1,2) = 1
dla x2∊ <2,3) = 2
dla x2∊ <3,4) = 3
Graficznie jest przedstawiony tylko wykres funkcji f(x) = E(x)


 początkami kolejnych
przedziałów funkcji
tak samo będzie w przypadku E(x2) tylko oczywiście inną funkcję bierzesz
początkami kolejnych
przedziałów funkcji
tak samo będzie w przypadku E(x2) tylko oczywiście inną funkcję bierzesz 

 tak będzie wyglądala część E(x2) dla x∊<0;1)?
tak będzie wyglądala część E(x2) dla x∊<0;1)?

 zielona prosta (y=x) to prosta 'pomocnicza'
zielona prosta (y=x) to prosta 'pomocnicza'
 ależ nie; a=√2 b=√3
i symetria względem OY
[x2] = 0 dla x∊(−1;1)
[x2] = 1 dla x∊(−√2; −1>∪<1;√2)
ależ nie; a=√2 b=√3
i symetria względem OY
[x2] = 0 dla x∊(−1;1)
[x2] = 1 dla x∊(−√2; −1>∪<1;√2)
 to było E(x)
analogicznie E(x2) będzie miało postać:
(zielona krzywa y=x2 to krzywa pomocnicza)
to było E(x)
analogicznie E(x2) będzie miało postać:
(zielona krzywa y=x2 to krzywa pomocnicza)
 x2 ≥ 1 ⇒ x ∊ (−∞;−1>u<1;∞)
x2 < 2 ⇒ x ∊ (−√2;√2)
o to chodzi?
y = 1 dla x ∊(−√2;−1>u<1;√2)
x2 ≥ 1 ⇒ x ∊ (−∞;−1>u<1;∞)
x2 < 2 ⇒ x ∊ (−√2;√2)
o to chodzi?
y = 1 dla x ∊(−√2;−1>u<1;√2)
 tylko porządniej to można zapisać
[x2] = 1 ⇔ 1 ≤ x2 < 2 ⇔ [ x2≥1 ∧ x2<2 ] ⇔ [ x2−1≥0 ∧ x2−2<0 ] ⇔
x∊(−∞;−1>∪<1;+∞) ∧ x∊(−√2;√2) ⇔
x∊[(−∞;−1>∪<1;+∞)]∩(−√2;√2) ⇔ x∊(−√2;−1>∪<1;√2)
tylko porządniej to można zapisać
[x2] = 1 ⇔ 1 ≤ x2 < 2 ⇔ [ x2≥1 ∧ x2<2 ] ⇔ [ x2−1≥0 ∧ x2−2<0 ] ⇔
x∊(−∞;−1>∪<1;+∞) ∧ x∊(−√2;√2) ⇔
x∊[(−∞;−1>∪<1;+∞)]∩(−√2;√2) ⇔ x∊(−√2;−1>∪<1;√2)



 tak to będzie wyglądało?
tak to będzie wyglądało?
 Dzięki za wskazówkę
Dzięki za wskazówkę  Logarytmów też nie miałem, dlatego teraz mam takie kombo: wartość
bezwzględna + logarytmy...
Logarytmów też nie miałem, dlatego teraz mam takie kombo: wartość
bezwzględna + logarytmy...

 a E(logax) przyjmuje ujemne ... i to straszliwie krótkie przedziały będą
a E(logax) przyjmuje ujemne ... i to straszliwie krótkie przedziały będą
 oba warunki muszą być spełnione
oba warunki muszą być spełnione





 dziękuję Ci bardzo za pomoc, trzeba iść spać, dobranoc.
dziękuję Ci bardzo za pomoc, trzeba iść spać, dobranoc.
