odcinek olaa: Dany jest odcinek AB o długości 58. Na odcinku AB znajdź taki punkt M, aby suma pól kwadratu o boku AM i trójkąta równobocznego o boku MB była najmniejsza. Oblicz długość odcinka AM

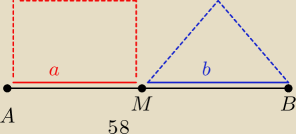
aniabb: a+b = 58 ⇒ a=58−b P = a² + b²√3/2 min (58−b)² + b²√3/2 3362 −116b +(1+√3/2)b² min w wierzchołku

	116		116		116(2−√3)
b=		=		=
	2(1+√3/2)		2+√3		4−3

b=116(2−√3) ≈31 punkt M jest około 31j. od B

irena_1: Aniu! Pole trójkąta równobocznego o boku b to

b2√3
4

a nie

b2√3
2

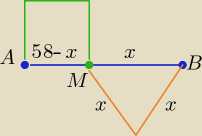
.: |AM|= 58−x x∊(0,58)

	x2√3		1		1
f(x)= (58−x)2 +		= x2−116x+582+		√3 x2= (1+		√3)x2−116x+582
	4		4		4

	4+√3
f(x)= (		)x2−116x+582
	4

parabola ramionami do góry, f(x) osiąga minimum dla odciętej wierzchołka

	−b
xmin=		=.......... (rachunki niezbyt przyjazne
	2a

.:

	a2√3
P(trójkąta równobocznego) =
	4

.: Na rysunku aniabb widnieje prostokąt

aniabb: przecież wiem ale co zrobić że nie ma opcji popraw

...o lol: aniabb jest superrr chcałbym mieć taką wiedzę jak ta wspaniała dziewczyna

.: Porządnie rysować ! i tyle

aniabb: bo na pomysł dorysowania wpadłam na końcu, jak już miałam obrazek i obliczenia i mi się nie zmieścił

.:

...o lol: to sam sobie rysuj , co już się jej pomylić nie można nawet najlepszemu sie zdaza, jak jestes taki mądry/a to sobe zam rysuj

.: