m xen: Oblicz pole figury określonej przez nierówność podaną w linku. E=97 http://latex.codecogs.com/gif.latex?\left&space;|y&space;\right&space;|&space;+&space;\frac{1}{e}{}&space;\leq&space;e^-&space;^\left&space;|x&space;\right&space;| proszę o pomoc

Basia:

	1
|y|+		≤ e−|x|
	e

1. x≥0 i y≥0

	1
y +		≤ e−x
	e

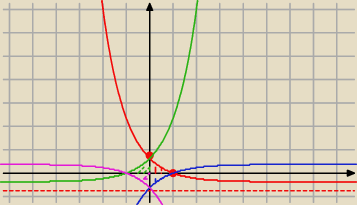
y ≤ e^−x − e⁻¹ e^−x−e⁻¹=0 e^−x = e⁻¹ x = 1 czerwony wykres i wszystko co poniżej, ale tylko w I ćwiartce czerwona kropka na OY = 1−e⁻¹, na OX = 1 P₁ = ₀∫¹(e^−x − e⁻¹)dx = [−e^−x − e⁻¹x]₀¹ = [−e⁻¹−e⁻¹*1] − [−e⁰ − e⁻¹*0] =

	2
−2e−1+1 = 1 −
	e

2. x≥0 i y<0 −y + e⁻¹ ≤ e^−x y ≥ −e^−x+e⁻¹ niebieskie w IV ćwiartce symetryczny do (1) względem OX P₂ = P₁ 3. x<0 i y≥0 y + e⁻¹ ≤ e^x y ≤ e^x−e⁻¹ zielony w II ćwiartce symetryczny do (1) względem OY P₃ = P₁ 4. x<0 i y<0 −y+e⁻¹ ≤ e^x y ≥ −e^x+e⁻¹ fioletowy w III ćwiartce P₄=P₁

	8
P = 4*P1 = 4 −
	e