Udowodnij,że... Mati: Udowodnij, że M jest punktem leżącym na przeciwprostokątnej AB trójkąta prostokątnego ABC to (AM)²*(BC)²+(BM)²*(AC)²=(CM)²*(AB)²

Mati:

Mati: Co trudne?

Mati_gg9225535: M to dowolnie położony punkt?

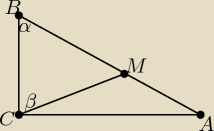
Vax: Oznaczenia jak na rysunku, stąd łatwo dostajesz <BMC = 180−α−β , <ACM = 90−β , <BAC = 90−α oraz <CMA = α+β, mając wszystkie kąty uzależniasz z twierdzenia sinusów długości odcinków AM , BC , BM , AC , MC od sinusów,cosinusów danych kątów oraz długości odcinka |AB|, po wstawieniu tego do tezy |AB|⁴ nam się skraca i dostajemy równoważnie jedynkę trygonometryczną.

Mati: Zadanie zostało przepisane całe z książki. Moim zdaniem punkt M to dowolnie położony punkt na przeciwprostokątnej trójkąta prostokątnego ABC. Dzięki za odpowiedź.