wtf midlee: Wykaz, że sinx + cosx > 1 gdy jedna z przyprostokątnych trójkąta prostokątnego ma długość a i przy niej znajduje się kąt x. jeśli sin²x + cos²x = 1 to jak sinx + cosx >1?

Andrzej: tak, że na przykład sinx = 0.8 a cosx = 0.6 0.64 + 0.36 = 1

Aga1.:

	b
tgx=		⇒b=atgx
	a

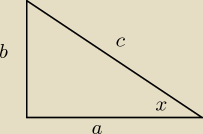
c²=a²+b² c²=a²+a²tg^x c=√a²(1+tg²x=a√1+tg²x

	b		atgx
sinx=		=
	c		c

	a
cosx=
	c

	atgx		a		1+tgx
sinx+cosx=		+		=		>1
	a√1+tg2x		a√1+tg2x		√1+tg2x

AC: Ponieważ, 0 < x < 90⁰⇒ sinx;cosx > 0 ⇒ 2sinx*cosx >0 ⇒ ⇒sin²x +cos^x +2sinx*cosx > 1 ⇒ ⇒(sinx +cosx)² > 1⇒ sinx +cosx > 1 co kończy dowód

AC: tam ma być po sin²x cos²x