pomocy!!! pomocy: jak wyznaczyc asymptoty takiej funkcji :

	1
f(x)= e(		)−x
	x

	1
tam jest do potegi
	x

Basia: f(x) = e^1/x −x D = R\{0} lim_x→0⁻ [ e^1/x−x] = e^−∞ − 0 = 0−0=0 lim_x→0⁺ [ e^1/x−x] = e^+∞ − 0 = +∞−0=+∞ masz asymptotę pionową prawostronną x=0

	f(x)		e1/x		e0
limx→±∞		= limx→±∞		− 1 =		− 1 = 0−1=−1
	x		x		±∞

lim_x→±∞[f(x)+x] = lim_x→±∞ e^1/x = e⁰ = 1 masz asymptotę ukośną obustronną y = −x+1

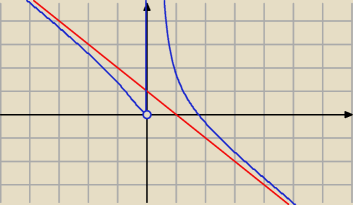Basia: tak wygląda wykres