F-ja malejąca, rosnąca. fi: Co robię źle? Wyznacz dziedzinę funkcji oraz przedziały na których dana funkcja jest malejąca lub rosnąca: f(x)=x/(x−2) y'=[(x)'*(x−2)−x*(x−2)']/(x−2)² y'=−2/(x−2)² −(x−2)²=0 −x²+4x−4=0 Δ=0 x=2 f malejąca R − {2} Odpowiedź ma być: f malejąca (−∞,−2)v(2,+∞) f rosnąca (−2,2)

Mati_gg9225535:

	x		x−2+2		x−2		2		2
y=		=		=		+		= 1+
	x−2		x−2		x−2		x−2		x−2

	2
rysujesz wykres y=		a potem przesuwasz o wektor Tu=[2,1] i odczytujesz wszystko z
	x

wykresu moja propozycja

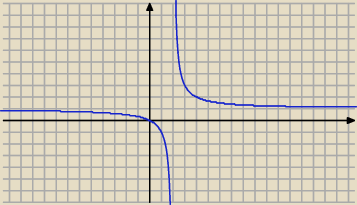
aniabb: mianownik ≠0 więc f' = 0 jak licznik =0 w liczniku zostało ci tylko −2 więc dla x∊D funkcja malejąca f malejąca (−∞,2)v(2,+∞) zresztą jak na hiperbolę przystało ....

fi: mam do tego użyć pochodnych.

aniabb: dotąd masz dobrze y'=−2/(x−2)² dalej wg mojego

fi: Rozwiązanie w książce jest inne, też mi wyszło tak jak Tobie.

aniabb: może błąd w przepisywaniu ? poza tym źle liczyłaś miejsce zerowe

fi: funkcję rosnącą też niechcący przepisali? dlaczego źle?

aniabb: bo w liczniku masz tylko −2

	−2
y' =		= 0 x∊∅
	(x−2)2

fi: nie mogę obustronnie podnieść do potęgi −1 i pomnożyć razy 2? co w tym jest źle?

aniabb: bo obustronnie to 0⁻¹ = ∞

aniabb: a tak naprawdę dowolna liczba czyli nieoznaczoność

aniabb: dlatego wbijają cały czas wierszyk .. ... pamiętaj cholero nie dziel przez zero

fi: obustronnie razy (x−2)⁴ to wyjdzie to samo Ale pierwszy raz słysze o tym 0⁻¹

fi: dobra, to jest tutaj najmniej ważne − nadal nie mam poprawnego roziwązania

aniabb: sprawdź może wzór funkcji nie taki..

aniabb: jak chcesz funkcję która pasuje do Twojego rozwiązania to np y=|(x+2)/(x−2)|

fi: sprawdzałam kilka razy i sprawdzałam też rozwiązanie. Tu nie chodzi o to żeby mi się podobało tylko żeby było dobrze −.−

aniabb: popatrz na wykres funkcji ... masz policzone dobrze .. gdy f(x)=x/(x−2) to f malejąca (−∞,2)v(2,+∞)

PW: Realizując swoje "odchylenie teoretyczne" muszę powiedzieć, że napis f malejąca (−∞,2)v(2,+∞) jest mylący, jeżeli nie wręcz niepoprawny. Badana funkcja jest malejąca na przedziale (−∞,2) i malejąca na przedziale (2,+∞) , natomiast w całej dziedzinie (−∞,2)∪(2,+∞) nie jest monotoniczna, co widać na rysunku anibb.

Aga1.: PW, masz rację, zawsze jest bezpieczniej przy monotoniczności nie łączyć przedziałów sumą,tylko oddzielać je przecinkiem i formułować odp. Np. Funkcja jest rosnąca w każdym z przedziałów i wymienić przedziały. W powyższym przykładzie za odp. 0 punktów. Poprawną odp. podał PW.