Rozwiązywanie nierówności wielomianowych PanTomBudujeDom: Witam Dany jest wielomian W(x)=x⁴+x²+ax+b , x∊R Wyliczyłem parametry a,b, więc pominę ten podpunkt zadania − jest na pewno dobrze. 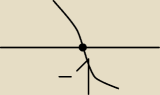a =0 b= −2 Problem mam w podpunkcie c) c) Dla wyznaczonych a i b rozwiąż nierówność W(x) ≤ x⁴+x³ Rozwiązuje to tak: x⁴+x²−2 ≤ x⁴+x³ x⁴−x⁴−x³+x²−2≤0 −x³+x²−2≤0 Liczba (−1) jest pierwiastkiem, więc po rozkładzie na czynniki pierwsze (x+1)(−x²+2x−2)≤0 Delta jest ujemna, więc pierwiastkiem będzie tylko − 1 i rysuję...(rysunek wyżej) Odp. x∊<−1,+∞) W odpowiedziach natomiast mamy od (−∞,−1>. A przecież jeżeli a <0 rysujemy wykres od dołu z prawej strony... Będę wdzięczny za wytłumaczenie.

Artur_z_miasta_Neptuna: mozliwy błąd w książce −−− Twój tok rozumowania (dla tak przedstawionej nierówności) jest prawidlowy

PanTomBudujeDom: Dziękuję

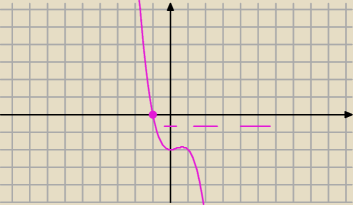Aga1.: Twoja odp. jest poprawna, chyba, że źle obliczyłeś a i b.

PanTomBudujeDom: Bardzo przejrzysty rysunek Podpunkt a) brzmi: a) Wyznacz a i b wiedząc, że wielomian jest podzielny przez x²−1 Policzyłem jeszcze raz dla pewności i a = 0; b= −2 Błąd w książce. Chciałem się upewnić Dziękuję