xxx Magda: 1. Dany jest wielomian W(x)=x⁴−4x²+kx+m a) wyznacz parametry k, m, tak aby reszta z dzielenia wielomianu W przez dwumian (x+2) wynosiła −3, a reszta z dzielenia wielomainu W przez dwumian (x−1) wynosiła 6. b) Dla k=0 Λ m=0 rozwiąż nierówność W(X)<0 2. Naszkicuj w układzie współrzędnych figurę okresloną układem nierówności x²+y²−10x≥−9 x²+y²−10x≤0 Oblicz pole tej figury. 3. Znajdź równanie stycznej do okręgu o równaniu (x−6)²+(y−8)²=20 poprowadzonej w punkcie K=(8,12)

Basia: W(x) = (x−2)*P(x) − 3 W(2) = 0*p(x)−3 W(2) = −3 −−−−−−−−−−−−−−− W(x) = (x−1)*Q(x)+6 W(1) = 0*Q(x)+6 W(1)=6 −−−−−−−−−−−−−−−−−− W(2) = 2⁴−4*2²+k*2+m = 16−16+2k+m = 2k+m 2k+m = −3 W(1) = 1⁴−4*1⁴+k*1+m = 1−4+k+m = k+m−3 k+m−3=6 k+m=9 musisz rozwiązać układ równań (niebieskich) k=0 i m=0 ⇒ W(x) = x⁴−4x² x⁴−4x²<0 x²(x²−4)<0 x²(x−2)(x+2)<0 x² ≥ 0 czyli (x−2)(x+2)<0 potrafisz dokończyć ?

Basia: (x−5)² = x² − 10x + 25 x² − 10x = (x−5)² − 25 x² + y² − 10x = (x−5)² − 25 + y² = (x−5)² + y² − 25 (x−5)² + y² − 25 ≥ −9 (x−5)² + y² − 25 ≤ 0 (x−5)² + y² ≥ 16 (x−5)² + y² ≤ 25 równanie (1) opisuje okrąg S(5,0) i r₁=4 i jego zewnętrze równanie (2) opisuje okrąg S(5,0) i r₂=5 i jego wnętrze układ równań opisuje więc pierścień kołowy S(0,5) r₁=4 r₂=5 P = πr₂² − πr₁² = π(r₂²−r₁²) podstaw i policz

Basia: równanie (x−6)²+(y−8)² = 20 opisuje okrąg o środku w punkcie S(6,8) i promieniu r=√20=√4*5=2√5 K(8,12) napisz równanie prostej KS styczna k to prosta ⊥ pr.KS i przechodząca przez punkt K

Magda: Basiu bardzo Ci dziękuję za wskazówki ale bardzo bym Cie prosiła o sprawdzenie. 1a) rozwiązałam ten układ i wyszło k=−14 m=25 dobrze tylko mam pytanie czemy tam jest W(1) a nie W(−1) 1b) x<2 i x<−2czyli x∊(−∞, 2) dobrze tylko mam pytanko dlaczego tu jest taki znak ≥ x2 ≥ 0 2. Pole wyszło mi 9π dobrze Basiu ale nie wiem jak zrobić rysunek pomóż

	1
3. równanie prostej KS wyszło y=2x−4 a stycznej k wyszło y=−		x+16 dobrze
	2

Basiu jak bedziesz mogła to spójrz proszę też na inne moje zadanka które wczoraj dodałam, dostałam podpowiedzi ale nadal wszystkiego nie rozumiem, a ty tak dobrze tłumaczysz. Bardzo dziekuje

Magda: Inne zadanka pomógł rozwiązać mi Bogdan jestem bardzo wdzięczna

Magda: tylko Basi jeszcze nie ma czy Bogdan mógłbyś mi sprawdzić te zadanka też

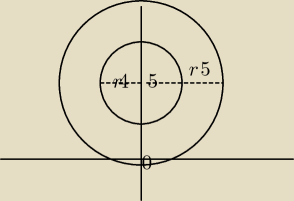
Magda: Czy ten rysunek w 2 zadaniu to ma tak wyglądać

Magda: sprawdzcie proszę

Basia: Magda, w tym pierwszym źle przeczytałam. To ma być W(−2) a nie W(2). Trzeba to poprawić. Na rysunku trzeba ten pierścień zacieniować. Resztę przeliczę za chwilę.

Basia: Zadanie 3 jest dobrze. Drugie zaraz Ci narysuję, a pierwsze napiszę od poczatku.

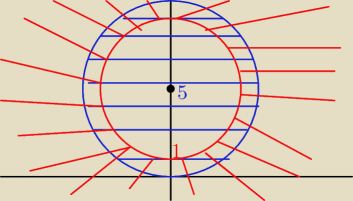
Basia: Twój pierścień to część wspólna "niebieskiego" (wnętrze + okrąg koła o promieniu 5) i "czerwonego" (zewnętrze i okrąg koła o promieniu 4) Pole masz dobrze policzone.

Basia: Zadanie 1. W(x) = (x+2)*P(x) − 3 W(−2) = (−2+2)*P(x) − 3 W(−2) = 0*P(x) − 3 W(−2) = −3 −−−−−−−−−−−−−−−− W(x) = (x−1)*Q(x) + 6 W(1) = (1−1)*Q(x) + 6 W(1) = 0*Q(x) + 6 W(1) = 6 −−−−−−−−−−−−−−−−−−−− W(−2) = (−2)⁴ − 4*(−2)² + k*(−2) + m = 16 − 16 − 2k + m = −2k + m −2k+m=−3 −−−−−−−−−−−−−−−−−−− W(1) = 1⁴ − 2*1² + k*1 + m = 1 − 2 + k + m = k + m −1 k+m−1=6 k+m=7 −−−−−−−−−−−−−−−− −2k+m=−3 k+m=7 /*2 −2k+m=−3 2k+2m=14 −−−−−−−−−−−−−−−−−− 3m=11 m=¹¹₃ k+¹¹₃ = 7 k = ²¹⁻¹¹₃ k=¹⁰₃

Basia: Zadanie 1b. x²≥0 (większe lub równe 0) bo dla x=0 x²=0 a dla x≠0 x²>0; razem x^≥0 x²−4<0 (x−2)(x+2)<0 x−2<0 ∧ x+2>0 ∨ x−2>0 ∧ x+2<0 x<2 ∧ x>−2 ∨ x>2 ∧ x<−2 niemożliwe x>−2 ∧ x<2 x∊(−2;2)

Magda: Bardzo Ci dziękuję Basiu, pozdrawiam