f.kwadratowa maciek: Osią symetri wykresu funkcji kwadratowej f jest prosta o równaniu x=4. Dla argumentów 2 i 3 wartości funkcji f są odpowiednio równe −5 i 1. Rozwiąż nierówność f²(x) +2f(x) −15≥0

krystek:

−b
	=4
2a

f(2)=−5 f(3)=1 znajdziesz wzór funkcji y=ax²+bx+c Następnie podstawiasz do tej nierówności

Eta: z treści zadania: p=x_w= 4 i f(2)= −5 i f(3)=1 q= y_w f(x)=a(x−4)²+q −5= 4a+q 1 = a+q −−−−−−−−− rozwiąż układ otrzymasz a= −2 q= y_w= 3 f(x)= − 2x²+16x −29 teraz przekształcasz lewą stronę nierówności tak: ( będzie łatwiej) f²(x) +2f(x) +1 −16 = (f(x)+1)² −16 = [f(x)+17][f(x)−15] ≥0 dokończ ........

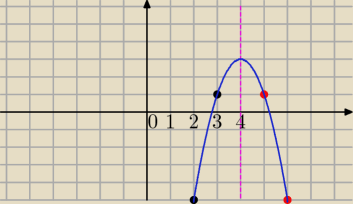
Mila: 1) wzór funkcji f(x)=ax²+bx+c x_w=4 wierzchołek paraboli leży na jej osi symetrii

	−b
xw=		=4⇔b=−8a
	2a

f(2)=−5⇔a*2²+b²+c=5⇔4a+2b+c=−5 f(3)=1⇔a*3²+b*3+c=1⇔9a+3b+c=1 Mamy układ:b=8a 4a+2b+c=−5 9a+3b+c=1 stąd a=−2, b=16, c=−29 f(x)=−2x²+16x−29 2) nierówność: f²(x) +2f(x) −15≥0 podstawienie f(x)=u u²+2u−15≥0 ; Δ=64 u₁=−5 lub u₂=3 ⇔u²+2u−15=(u+5)*(u−3)=(f(x)+5)(f(x)−3)⇔ (−2x²+16x−29+5)(−2x²+16x−29−3)≥0 (−2x²+16x−24)(−2x²+16x−32)≥0 rozłóż na czynni i rozwiąż, wychodzą ładne liczby

Eta: Poprawiam , bo wkradł mi się błąd bo (f(x)+1)²−16= (f(x)+1)²−4² ...= [f(x)+1+4][f(x)+1−4]= [f(x)+5][f(x)−3) ≥0

Eta: Hej Mila ........... popsułaś zabawki

Mila: Eto, witaj. Nie widziałam Twojego wpisu, bo przecież nie dublowałabym rozwiązania.

Eta:

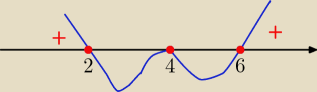
Eta: No to dokończę (x²−8x+12)(x²−8x+16)≥0 (x−2)(x−6)(x−4)²≥0 x€ (−∞>2 U <6,∞) U {4}