| 1 | ||
jak poradzic sobie z Im | = 0,5 ? pomocy  | |
| z |
| 1 | ||
ln | = 0,5 | |
| z |
| 1 | ||
e0,5 = | ||
| z |
| 1 | ||
√e = | ||
| z |
| 1 | ||
z = | = e−1/2 | |
| √e |
| 1 | ||
Im | = 0,5 | |
| z |
| 1 | 1 | x−iy | |||
= | = | = | |||
| z | x+iy | (x+iy)(x−iy) |
| x−iy | x−iy | ||
= | = | ||
| x2 − i2y2 | x2+y2 |
| x | y | ||
−i* | |||
| x2+y2 | x2+y2 |
| y | 1 | ||
= | |||
| x2+y2 | 2 |
| y | 1 | |||
− | = | |||
| x2+y2 | 2 |
 mozliwe ze bede miala jeszcze pytania i bylabym
wdzieczna gdybys mi z nimi pomogla
mozliwe ze bede miala jeszcze pytania i bylabym
wdzieczna gdybys mi z nimi pomogla 

 z = x+iy
z−2 = (x−2)+iy
|z−2| = √(x−2)2+y2
√(x−2)2+y2 ≥ x
√(x−2)2+y2 ≥ 0 dla każdej pary (x,y)
czyli dla każdego x≤0 nierówność jest prawdziwa
co daje oś OY i półpłaszczyzną od niej w lewo
dla x>0 można podnieść obustronnie do ()2
(x−2)2+y2 ≥ x2
x2−4x+4+y2−x2≥0
y2 ≥ 4x−4
jak poprzednio dla 4x−4≤0 nierówność jest prawdziwa co daje
4x≤4 czyli x≤1
a to jest prosta x=1 i półpłaszczyzna od niej w lewo
dla x>1
y2 ≥ 4x−4
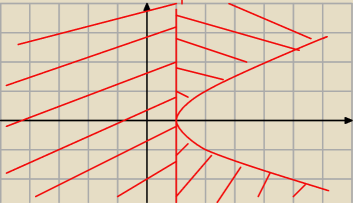
czyli parabola, której osią symetrii jest oś OX, wierzchołek W(1,0), ramiona w prawo
i to wszystko co na zewnątrz niej
bo
y2≥4x−4 ⇔ y≥√4x−4 lub y≤ −√4x−4
z = x+iy
z−2 = (x−2)+iy
|z−2| = √(x−2)2+y2
√(x−2)2+y2 ≥ x
√(x−2)2+y2 ≥ 0 dla każdej pary (x,y)
czyli dla każdego x≤0 nierówność jest prawdziwa
co daje oś OY i półpłaszczyzną od niej w lewo
dla x>0 można podnieść obustronnie do ()2
(x−2)2+y2 ≥ x2
x2−4x+4+y2−x2≥0
y2 ≥ 4x−4
jak poprzednio dla 4x−4≤0 nierówność jest prawdziwa co daje
4x≤4 czyli x≤1
a to jest prosta x=1 i półpłaszczyzna od niej w lewo
dla x>1
y2 ≥ 4x−4
czyli parabola, której osią symetrii jest oś OX, wierzchołek W(1,0), ramiona w prawo
i to wszystko co na zewnątrz niej
bo
y2≥4x−4 ⇔ y≥√4x−4 lub y≤ −√4x−4