geometria Madzia: Udowodnić, że trójkąt jest prostokątny wtedy i tylko wtedy, gdy 2R+r=s (s to suma boków trójkata)

think: Madzia, a R i r to odpowiednio promień okręgu opisanego i wpisanego w ten trójkąt?

Artur_z_miasta_Neptuna: a znasz wzory na wyznaczanie promienia okręgu wpisanego i opisanego na trójkącie

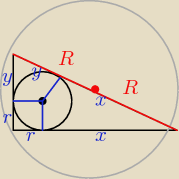
aniabb: s= r+x+x+y+y+r=2r + 2R + 2R = 2r+4R czyli nie suma boków, a połowa obwodu s/2 = r+2R

Artur_z_miasta_Neptuna: aniu ... wybacz, że się wtrącę ... ale to chyba nie jest dowód

PW: Dowód "w jedną stronę" (aniabb liczy, że stosowne komentarze w rodzaju "przeciwprostokątna trójkąta wpisanego jest średnicą" czy "odcinki stycznych poprowadzonych z jednego punktu są równe" adept dopisze sobie sam, nie można wszystkiego "na talerzu"). Dowód twierdzenia odwrotnego czeka na chętnych.

aniabb: a ja nie chciałam nic dowodzić tylko pokazać jak to wygląda i przy okazji wyszło mi że to pół obwodu