 Podaję plan rozwiązania, nie widzę prostszego rozwiązania.
Oznaczenia:
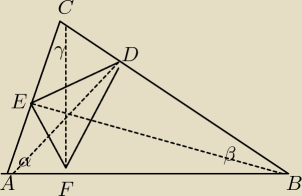
AD = h1 , BE = h2 , CF = h3
1. Obliczyć pole trójkąta ABC wzorem Herona (= S)
2. Obliczyć kąty α , β i γ tw. cosinusów
3. Obliczyć wysokości trójkąta ABC
h1 = 2*S/BC , h2 = ... , h3 = ...
4. AF = AC*cos(α) , AE = AB*cos(α)
EF2 = AF2 + AE2 − 2*AF*AE*cos(α)
Analogicznie obliczyć DF i DE
5. Obliczyć pole trójkąta DEF (wzór Herona) (= S1)
6. Szukany promień
Podaję plan rozwiązania, nie widzę prostszego rozwiązania.
Oznaczenia:
AD = h1 , BE = h2 , CF = h3
1. Obliczyć pole trójkąta ABC wzorem Herona (= S)
2. Obliczyć kąty α , β i γ tw. cosinusów
3. Obliczyć wysokości trójkąta ABC
h1 = 2*S/BC , h2 = ... , h3 = ...
4. AF = AC*cos(α) , AE = AB*cos(α)
EF2 = AF2 + AE2 − 2*AF*AE*cos(α)
Analogicznie obliczyć DF i DE
5. Obliczyć pole trójkąta DEF (wzór Herona) (= S1)
6. Szukany promień
| EF*DF*ED | ||
R = | ||
| 4*S1 |