napisz równanie okręgu o promieniu 5, do którego należą punktyAiB A(-6,0)B(4,0
andrzej:
19 lis 21:46
Beti: podstaw współrzędne obu punktów do równania okręgu −− powstana dwa równania z niewiadomymi a i
b. Jak rozwiążesz te równania (układ równań), to będziesz miał wsp. środka okręgu.
19 lis 21:49
Aga1.: Równanie okręgu
(x−a)2+(y−b)2=r2
r=5
(−6−a)2+b2=25
(6−a)2+b2=25
Rozwiąż
19 lis 21:51
Mila:
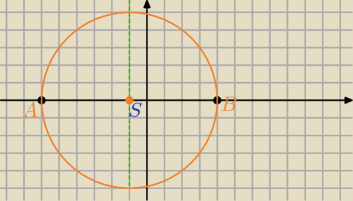
S(a,b)−środek okręgu leży na symetralnej AB, AB to cięciwa⇔a=−1
r=5
odległość środka okręgu od punktów jest równa 5
(a−(−6))
2+(b−0)
2=5
2
(a−4)
2+(b−0)
2=5
2
(−1−4)
2+b
2=25
b
2=0⇔b=0
S=(−1;0)
Równanie okręgu:
(x+1)
2 y
2=25
19 lis 23:11
Mila: (x+1)2+y2=25
19 lis 23:12
Mila: ?
19 lis 23:31