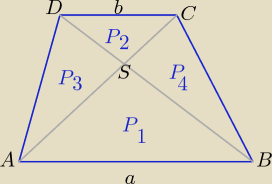
planimetria Rodney: W trapez o polu 168 i ramionach 13 i 15 mozna wpisac okrag. Przekatne dziela ten trapez na 4 trojkaty. Oblicz pole kazdego z nich. Wiem, ze: a+b=15+13=28

	1
168=		*28*h, wiec h=12
	2

Z tego co wiem to chyba tez te dwa trojkaty "po bokach" maja takie same pola. Co dalej? Prosze o jakies wskazowki

irena_1: Narysuj ten trapez i dwie wysokości z końców krótszej podstawy. Podzielą one dłuższą podstawę a na odcinki x, b, y (b to krótsza podstawa) x²+12²=13² x=5 y²+12²=15² y=9 a+b=28 a=b+14 b+b+14=28 b=7 a=21 Trójkąty, których podstawami są podstawy trapezu, są podobne. Skala jest równa 3. Wysokość jest więc podzielona w stosunku 1:3

	3
ha=		*12=9
	4

	1
hb=		*12=3
	4

	21*9
P1=		=94,5
	2

	7*3
P2=		=10,5
	2

	168−(94,5+10,5)		168−105		63
P3=P4=		=		=		=31,5
	2		2		2

meta: Z tw. Pitagorasa obliczysz a i b : a= 21 i b=7

	a
skala podobieństwa trójkątów ABS i CDS k=		=3
	b

P1
	= k2=9 to P1= 9P2 i P3=P4=k*P2=3P2
P2

P(t) = 9P₂+P₂+6P₂= 16P₂ 16P₂=168 teraz dokończ ....

meta:

Mila: http://www.zadania.info/9762890 Jest rysunek i wyjaśnienie.

Rodney: ooo, dziekuje bardzo kombinowalem jakos podobnie, ale jednak nie wpadlem na ten tok myslenia