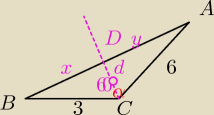
trojkat edumat: aniabb pomóż ! W trójkącie ABC dane są: miara kąta ACB wynosząca 120st., |AC| = 6, |BC| = 3. Dwusieczna kąta ACB przecina bok AB w punkcie D. a) Oblicz długość odcinka CD. b) Jaki jest związek między długościami promieni: okręgu opisanego na trójkącie ADC i okręgu opisanego na trójkącie DBC? Odpowiedź uzasadnij.

aniabb: twierdzenie cosinusow razy 3 będę za 2h to policzę

edumat: ok jestes wielka

edumat: jeszcze jakby kto mogl to zrobic...>> W równoległoboku ABCD przekątna DB ma długość 7. Wiedząc, że obwód równoległoboku wynosi 26, kat ABC=120st., oblicz długości boków równoległoboku.

xxxxxxx: fakultet marcowy

edumat: taaa ty klasa f g czy e?

aniabb: jestem

edumat: o to dobrze ze jestes ania masz jakies rozwiazanko moze?

edumat: i jeszcze to drugie zadanie ania jakbys miala ochote bo tez nie wiem jak rozkminic

aniabb: oki myślałam nad czymś przyjemniejszym niż cosinusy, ale chwilowo nie mam pomysłu więc muszę chyba rozpisać

edumat: ok moze byc dowolnie byle żeby było

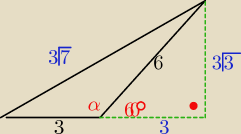
aniabb: przeciwkątna c² = 3²+6²−2*6*3*cos(120°) = 9+36−36(−1/2) = 45+18=63 c=3√7 y=3√7−x małe cosinusy x²=3²+d²−2*3*d*cos(60°) ⇒ x²=9+d²−3d y²=6²+d²−2*6*d*cos(60°) ⇒(3√7−x)² = 36 +d²−6d −−−−−−−−−−−−−−−−−−−− odejmujemy stronami 63−6√7x = 25 −3d d= 2√7x −38/3 x² = 9 +(2√7x −38/3)²−3(2√7x −38/3) i policz x ..potem d

edumat:

	2n2−3n+1
mam jeszcze cos takiego Dany jest ciąg (an) o wyrazie ogólnym: .an=
	2n−1

a) Uzasadnij, że wszystkie wyrazy ciągu (an) są liczbami naturalnymi. >>> to moge podzielic to przez siebie wychodzi n−1 a n nalezy do calkowitych dodatnich i n>badz rowne 1 wiec jest uzasadnione ze beda liczbami naturalnymi?

aniabb: ech..brzydki..

edumat:

aniabb: tak

aniabb: brzydki x wyszedł co to za zadania

edumat: ale co tak ...zgadzasz sie z tym co napisalem ad "mam jeszcze cos takiego Dany jest ciąg (an) o wyrazie ogólnym"...?

edumat: ania dziekuj Bogu ze nie jestes na moim fakultecie

edumat: tu sa te zadania co robie>>> http://word.office.live.com/wv/WordView.aspx?FBsrc=http%3A%2F%2Fwww.facebook.com%2Fdownload%2Ffile_preview.php%3Fid%3D472494842789663%26metadata&access_token=100004284129862%3AAVL2BSz03aZrBrkLBWNttP7-Lv_zyfWXB35AeIyE4-qlWg&title=rozszerzona.doc

edumat: jakbys jeszcze chciala ktores zrobic to bede bardzo wdzieczny

aniabb: zgadzam się z ciągiem

edumat: Losujemy jedną liczbę spośród liczb 1; 2; 3; ...; 1000. Oblicz prawdopodobieństwo wylosowania liczby podzielnej przez 4 lub przez 9. >>a to zadanie moge tak zrobic... 1000:4=250 tyle

	1
l.podziel. przez 4 (Pa=250/1000 =		1000:9=111(Pb=111/1000= tyle l. podziel przez 9 i
	4

czesc wspolna 1000:36=27 (Paib=0,027 czyli Pwyl tej liczby to Pa+Pb−Paib?

aniabb: Pole trójkąta 1/2 ah = 1/2 * 3 * 3√3 = 9√3/2

	abc		3*6*3√7
promień okręgu opisanego R=		=		=√21
	4P		18√3

	2P		9√3
promień okręgu wpisanego r=		=
	a+b+c		18+3√7

aniabb: poczekaj aż skończę pierwszy

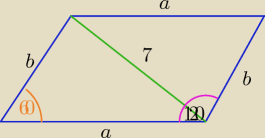
meta: 2a+2b=26 , to a+b=13 z tw. cosinusów

	1
72=a2+b2−2ab*cos60o , cos60o=
	2

a²+b²−ab= 49 (a+b)²−3ab= 49 13²−49=3ab ab= 40 a= 13−b , 0< b<13 (13−b)*b= 40 b= 5 lub b=8 no to a= 8 lub a=5 Równoległobok ma boki długości 8 i 5

edumat: aniabb: "poczekaj aż skończę pierwszy " pleć męska? "pierwszy">>?

aniabb: pierwszy przykład

edumat: ohhhhh ania ulzyło mi

aniabb: oo drugiego już nie muszę bo masz ciąg zrobiony samodzielnie... to teraz pr−wo

edumat: czytanie ze zrozumieniem kurde jutro bede miał na probnej maturze nie zdam!

aniabb: prawdopodobieństwo też OK

aniabb: wielomian chcesz?

edumat: jeszcze glupia izometrie ktorej nie lubie musze zrobic >>> Przekształcenie P określone jest w sposób następujący: P((x; y)) = (y + 2; x – 1), gdzie x, y R.. a) Wykaż, że przekształcenie P jest izometrią. b) W prostokątnym układzie współrzędnych narysuj trójkąt o wierzchołkach A = (−1; 2), B = (2; −4), C = (1; 5), a następnie znajdź jego obraz w przekształceniu P. c) Wyznacz równanie prostej zawierającej wysokość trójkąta ABC poprowadzoną na bok AB. d) Oblicz pole trójkąta A’B’C’, który jest obrazem trójkąta ABC w jednokładności o środku w punkcie (0; 0) i skali k = −5.

edumat: jaki wielomian?

aniabb: zadanie 8 z kartki

edumat: to punkt 4 i 2 podstawic zauwazyc ze 4:(2²)−2=2 czyli W(x)(x)=x czyli W(x)=x³−x²

edumat: *W(x) : P(x)=x

edumat: ?

aniabb: nie bo u ciebie 0 jest pierwiastkiem podwójnym W(x)=ax(x−1)²

edumat: dobrze zrobilem?

aniabb: i podstawiasz do tego (2;4) i wychodzi że a=2

aniabb: szukany wielomian to W(x) = 2x³−4x²+2x

edumat: aaaaa ale ty spostrzegawcza jestes a wiec jak jak odnalezc ten W(x)?

aniabb: o 21:25 masz

edumat: łokej to gitara a na tą izometrie zadanie 2 mogłabyś looknąć?

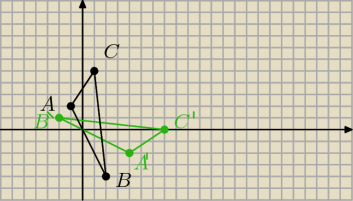
aniabb: izometria to funkcja która zachowuje odległości ..policz długości boków trójkąta ABC i A'B'C' i sprawdź czy są nadal takie same

Wojtek: !Aniabb Mogłabyś spojrzeć na pochodne czy dobrze obliczyłem?

aniabb: prosta zawierająca wysokość trójkąta z C to y=1/2 x +4,5