wykaz Rodney: Wykaż, że f(x)=x³+2x²+4x−2 ma dokladnie jedno miejsce zerowe. Probowalem zrobic ale nie wychodzi nic Da ktos wskazowke moze? Prosze nie dawac mi gotowych odpowiedzi

Vax: Pokaż, że ta funkcja jest ściśle rosnąca.

AC: Policz extrema, jeśli f_min * f_max > 0 to ma jedno miejsce zerowe, albo ze wzorów Cardano.

Artur z miasta Neptuna: Do uwagi Vax'a dorzuce jeszcze wlasnosc darboux ... w koncu scisle rosnaca jest takze 2^x a koejsca zerowego nie posiada

Vax: No miała być wskazówka

AC: Przecież funkcja nie musi być ściśle rosnąca i może mieć 1 miejsce zerowe. Przykład: y=x³ − x +1 ma 1 miejsce a jest przedział w którym maleje.

Rodney: AC: jesli chodzi o extrema to ta funkcja chyba nie ma zadnych pozostale wskazowki zaraz sprawdze ogolnie to moj matematyk chyba przegial dajac mi to zadanie w 2 klasie liceum ale coz... zdarza sie

Vax: AC, nigdzie nie pisałem, że to działa w obie strony. Jeżeli funkcja jest ściśle rosnąca i przyjmuje wartości dodatnie jak i ujemne, to musi mieć dokładnie jedno miejsce zerowe, nie pisałem, że działa to w drugą stronę

Mila: Rodnej, dobrze przepisałeś treść zadania?

Rodney: raczej tak Mila, a cos sie nie zgadza?

AC: skoro nie ma extremów i pochodna y' > 0 to kończy dowód.

Basia: czegoś tu kochani zabrakło: x−5 dla x<0 f(x) = x+5 dla x≥0 ta funkcja jest ściśle rosnąca, przyjmuje wartości dodatnie i ujemne, i nie ma miejsc zerowych no czego zabrakło ? jakich funkcji dotyczy własność Darboux ?

irena_1: Funkcja f(x) jest ciągła. f(−1)=−1+2−4−2=−5 f(1)=1+2+4−2=5 więc dla x ∊ (−1; 1) przyjmuje wszystkie wartości z przedziału (−5; 5). Funkcja ma więc miejsce zerowe. A ponieważ jest funkcją stale rosnącą, więc to miejsce zerowe jest jedyne.

AC: Basiu w zadaniu nie mówimy o dowolnej funkcji a o wielomianie stopnia 3 o którym wiemy, że jest funkcją klasy C^∞(R)

Mila: Przypominam, że zadanie jest na poziomie II klasy LO, tak napisał autor zadania.

Basia: 1.ależ AC wiem, że wiesz, tylko przywołując prawo trzeba powiedzieć, że ono działa dla funkcji ciągłych 2. Milu to chyba jakaś mniej typowa szkoła, Rodney jest wyraźnie oswojony z takimi pojęciami jak np.ekstrema

Basia: W(x)= x³+2x²+4x− 2 łatwiej zadaje się wykazać, że W(x) jest funkcją różnowartościową W(x₁) = W(x₂) ⇔ x₁³+2x₁²+4x₁−2 = x₂³+2x₂²+4x₂−2 (x₁³−x₂³)+2(x₁²−x₂²) + 4(x₁−x₂) = 0 (x₁−x₂)(x₁²+x₁x₂+x₂²) + 2(x₁−x₂)(x₁+x₂) + 4(x₁−x₂) = 0 (x₁−x₂)*[ x₁²+x₁x₂+x₂² + 2x₁+2x₂+4] = 0 x₁−x₂ = 0 lub x₁² + (x₂+2)x₁ + (x₂²+2x₂+4) = 0 traktuję x₁ jak zmienną; x₂ jak parametr aby to zachodziło musiałoby być Δ≥0 Δ= (x₂+2)² − 4(x₂²+2x₂+4) = x₂²+2x₂+4 − 4x₂² − 8x₂ − 16 = −3x₂²−6x₂−12 ≥0 /: (−3) x₂² + 2x₂ + 4 ≤ 0 Δ₂ = 4−16<0 a więc to jest niemożliwe czyli W(x₁)=W(x₂) ⇔ x₁−x₂=0 ⇔ x₁=x₂ czyli W(x) jest różnowartościowa (na pewno można jakoś pobawić się wzorami skróconego mnożenia, żeby to pokazać, ale nie chciało mi się; dlatego Δ) ponieważ W(0) = −2<0 i W(1) = 1*3²−2 = 7>0 i W(x) jest ciągła to musi przyjmować (z tw. o wartościach pośrednich) dla jakiegoś x₀∊(0,1) wartość 0 a ponieważ jest różnowartościowa to może wartość 0 przyjmować tylko raz czyli x₀ jest jedynym pierwiastkiem tego wielomianu

Basia: W(1)=5 oczywiście, (pomyliłam na chwilę kartki) ale to nie ma znaczenia dla sensu rozwiązania

Basia: P.S. Oczywiście jeżeli policzymy pochodną mamy to wszystko natychmiast, ale Rodney prosił o rozwiązanie bez stosowania pochodnych

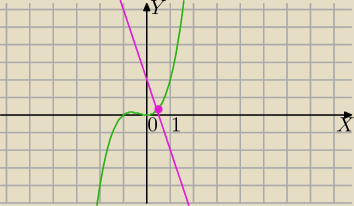
Mila: Graficznie: x³+2x²+4x−2 =0 g(x)=x³+x² zielony wykres: 2 miejsca zerowe wielomianu (x=−1 ; x=0) h(x)=−4x+2 9 różowy wykres

Mila: x³+2x²+4x−2 =0 równanie ma jeden pierwiastek rzeczywisty

PW: No i tak wspólnymi siłami doszliśmy do wniosku, że masz bardzo dobrego nauczyciela, który stawia zadania na odpowiednio wysokim poziomie, ale nie przesadza. Rozważmy funkcję g(x) = x³+2x²+4x Jest ona iloczynem funkcji x i pewnej funkcji kwadratowej, która przybiera tylko wartości dodatnie, i to większe od ... Jeżeli teraz weźmieny f(x) = g(x) −2, czyli "pociągniemy wszystko w dół o 2", to dalej ... Chciałeś pomysł, masz pomysł. Nie trzeba jeszcze nic wiedzieć o pochodnych.

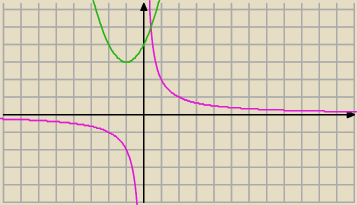Mila: PW, a co sądzisz o takim rozwiązaniu, generalnie nie lubię dzielić przez x, ale x=0 nie jest rozwiązaniem równania : x³+2x²+4x−2 =0 zatem: x(x²+2x+4)=2 /:x dla x≠0

	2
x2+2x+4=
	x

wykres funkcji kwadratowej i homograficznej znany uczniom klasy II.

PW: No też pięknie. Uczeń ma znać podstawowe wykresy i wyciągać wnioski z ich przebiegu. Zadanie okazało się nie takie trudne i możliwe do zrobienia kilkoma sposobami. Takie powinny być na maturze.

PW: Dla Rodneya mam zadanie (eksperci, wstrzymajcie się na razie) trochę trudniejsze, ale do zrobienia w podobny elementarny sposób: Udowodnij, że (x–2)(x–4)(x–5)(x–7) + 10 > 0 dla wszystkich rzeczywistych x. Daj znać, czy poszło.

pigor: ... a ja nic złego nie powiedziałbym będąc "tym " nauczycielem, gdyby Rodney w 2−ej klasie LO podszedł do tego jak do wielomianu i uzasadnił (pokazał mi) np. tak : f(x)= x³+2x²+4x−2, ponieważ f(−2)= −8+8−8−2= −10< 0 i f(−1)= −1+2−4−2= −5< 0 i i f( 0)= −2< 0 oraz f(1)=1+2+4−2= 5 >0 i f(2)= 8+8+8−2= 22 >0 ... itd, a wielomian jest funkcją ciągłą , to istnieje x_o ∊ (0 ;1) − jedyny pierwiastek rzeczywisty równania f(x)=0 . ...

AC: Jeśli weźmiesz taki wielomian: f(x)=x³−2x²+(11/9)x−2/9 f(0)=−2/9 f(1)=0 i w przedziale (0; 1) ma jeszcze 2 pierwiastki 1/3 i 2/3 a nie jeden.

PW: No dobrze, ale z ciągłości nie wynika jeszcze, że ten wielomian "nie szaleje" między 0 a 1 i nie przyjął tam trzykrotnie wartości 0. To itd ... słabo się broni. Trzeba by wykazać ściśle, że ten wielomian jest funkcją rosnącą, wtedy się zgadzam. Nie jestem nauczycielem, uczeń II klasy w listopadzie powinien wiedzieć, co to jest funkcja ciągła?

Mila: Uczeń w LO nie wie co to jest funkcja ciągła. Będzie wiedział wg nowego programu.

pigor: ... zgadzam się z wami, podoba mi się to , że ... szaleje wielomian ... ; a takich uwag właśnie, się spodziewałem , a wręcz oczekiwałem . ... ) a co z tą nierównością można już coś zaproponować, czy czekamy na Rodney−a

PW: Już nie czekamy, chyba nie jest zainteresowany. pigor, proponuj − jestem ciekawy, czy znajdzie się inny sposób niż ten, który znam.

AC: Ciekawe jaki znasz ja wymyśliłem taki. Robimy podstawienie: t=x−4,5 i otrzymujemy: (t+2,5)(t+0,5)(t−0,5)(t−2,5) + 10 > 0 ⇔ (t²−0,5²)(t²−2,5²) + 10 > 0 kolejne podstawienie u = t² − 3,25 daje nam: (u − 3)(u + 3) + 10 > 0 ⇔ u² + 1 > 0 co jest oczywistą prawdą.

PW: Ten też znam, można go nazwać inteligentnym wykorzystaniem symetrycznego parami położenia pierwiastków Inny sposób: wymnożyć te jednomiany odpowiednio dobranymi parami i zauważyć, że otrzymane funkcje kwadratowe różnią się o 6, a więc po podstawieniu mamy nierówność u(u−6)>−10, która też jest oczywista, bo parabola ma wierzchołek o drugiej współrzędnej −9. Tak więc można tę nierówność nawet "polepszyć" do postaci (x–2)(x–4)(x–5)(x–7) + 9 ≥ 0.

pigor: ... , bardzo podobnie , bo rozpisałem sobie wszystko ze wzorów Viete'a (w ... pamięci) tak : (x–2)(x–4)(x–5)(x–7)+10= (x–2)(x–7)*(x–4)(x–5)+10= (x²−9x+14)(x²−9x+20)+10= = (x²−9x)²+(14+20)(x²−9x)+14*20 +10= (x²−9x)²+2*17(x²−9)+17²+1= = (x²−9x+17)²+1>0 c.n.u. . ...

pigor: ... , może powiem jeszcze, że analogicznie podchodzę do zadań typu: Znajdź najmniejszą wartość tego typu wielomianu np. tu powyżej jest nią 1. −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− zaś wielomianu np. W(x)= (x–1)(x–2)(x–3)(x–4)+10 jest liczba 9, analogicznie wielomianu P(x)= (x+1)(x+2)(x–2)(x–3)+ 3 jest liczba . ...

PW: No i pięknie, "sprzedaliśmy" pewną godną polecenia metodę, ale Rodney nie jest zainteresowany, wygląda na to, że nas to bardziej obchodzi niż pytającego. Dziękuję w każdym razie za owocną wymianę przemyśleń.

dagaa: 4x² + 4x + 1 / x+5