moze ktos pomoc?
paula: w trapezie rownoramiennycm jedna z podstaw jest 2 razy dłuzsza od drugiej, a przekatna jest
dwusieczna kata przy dłuzszej podstawie. oblicz dlugosci bokow tego trapezu wiedzac, ze jego
pole jest rowne 9cm2. oblicz pole kola opisanego na tym trapezie.
+rysunek i obliczonka
19 maj 18:23
tim: Ja próbuję.
19 maj 18:27
paula: dzieki!
19 maj 18:36
tim:
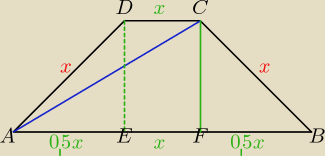
Kąty:
CAD α (Korzystając z tego, że AC jest dwusieczna)
CAB α
CBA 2α (Korzystając z tego, że trapez jest równoramienny)
BCA 180 − 2α − α = 180 − 3α (Korzystając z tego, że w trójkącie ABC musi być 180
O)
Zajmujemy się trójkątem AED:
Kąty:
DAE 2α (Jest to CAD + CAB)
EDA 180 − 90 − 2α = 90 − 2α (Korzystając z tego, że w trójkącie prostokątnym AED musi być
180
O)
Na mocy powyższej:
Kąty:
ADC 90 + 90 − 2α = 180 − 2α (Jest to ADE + CDE)
W każdym trapezie:
ADC = BCD, więc:
180 − 2α = 180 − 3α + ACD
ACD = α
Widzimy, że:
ACD jest równoramienny = AD = CD = CB
Wracamy do trójkąta DEA
AE
2 + DE
2 = AD
2
(0,5x)
2 + DE
2 = x
2
0,25x
2 + DE
2 = x
2
DE
2 = 0,75x
2
DE =
√0,75x2 =
√0,75x = 0,5x
√3
No dawaj dalej.
19 maj 18:41
paula: co dalej?
19 maj 18:57
tim: Masz już boki:
x, 2x
Ramiona:
x, x
Wysokość
0,5x√3
Podstaw do wzoru na pole i oblicz x.
19 maj 19:00
AS: Porównaj rozwiązanie w kaska
21 maj 15:39