określ dziedzinę wyrażenia wymiernego
Bu$kA;)): określ dziedzinę wyrażenia wymiernego
x 2−4x+5x3+3x2+3x+1
wiem już, że mianownik nie może się równac 0...
19 maj 18:16
Bu$kA;)): kurcze troche jest tam namieszane bardzo nie wiem dlaczego
licznik: x2−4x+5
mianownik: x3+3x2+3x+1
19 maj 18:18
tim: To jest jedyne założenie:
x3 + 3x2 + 3x + 1 ≠
19 maj 18:19
tim: 0
19 maj 18:19
Andrzej: tak jak poprzednio... w mianowniku nie może być zera.
x3+3x2+3x+1 ≠ 0 to po lewej stronie to wzór skróconego mnożenia
(x+1)3 ≠ 0
x+1 ≠ 0
x ≠ −1
19 maj 18:20
Bu$kA;)): dzięki

myslę, że z kolejnymi przykładami dam już sobię radę

19 maj 18:23
pawel: licznik 2x2−1 + x+2 + x+1
mianownik 4−x2 x−2 x+2 proszę o pomoc z góry dzięki....
20 lip 13:27
Bogdan:
| | 2x2 − 1 | | x + 2 | | x + 1 | |
Pawle, czy chodzi o wyrażenie: |
| + |
| + |
| ? |
| | 4 − x2 | | x − 2 | | x + 2 | |
Jak widzisz, dało się to tutaj zapisać.
Jakie jest polecenie w tym zadaniu?
20 lip 15:10
Michał: Określ dziedzinę wyrażenia wymiernego :
29 sty 18:15
Juras: ktoś się bawi w górnika

29 sty 18:16
mela:
patrzysz na mianowniki , muszą być różne od zera
x −2 ≠0 i x2−4≠0 => ( x−2)(x+2) ≠0 => x ≠2 lub x ≠ −2
Df= R \{−2,2}
29 sty 18:17
Michał: dzieki

a to, rozwiaz rownanie :
log
3 (2x
2 − 5) = 1 bo wiem jak rozwiazac normalne ale nie wiem jak do kwadratu

29 sty 18:22
mela:
Po pierwsze :
| | √10 | | √10 | |
założenie: 2x2 −5 >0 ( x − |
| )(x + |
| ) >0
|
| | 2 | | 2 | |
| | √10 | | √10 | |
założenie: x € (−∞, − |
| ) U ( |
| , ∞)
|
| | 2 | | 2 | |
teraz z def. logarytmu
2x
2−5= 3
1 => 2x
2 −8=0 => x
2−4)=0 => ( x−2)(x+2)=0
x = 2 v x= −2
obydwa są rozwiązaniami bo spełniają założenie
29 sty 18:36
29 sty 18:37
Michał: Dziękuję bardzo

29 sty 18:40
sewli: 2x2 + x +1/3x2−4x
1 paź 22:42
marta:
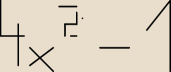
4x
23 paź 23:15
Nie piję bo matura:
(2x−1)(2x+1)
23 paź 23:15
Antek: Moze tak. Dlaczego tak pozno

4x
2−1=(2x−1)(2x+1) wzor a
2−b
2=(a−b)(a+b) i spac
23 paź 23:17
 myslę, że z kolejnymi przykładami dam już sobię radę
myslę, że z kolejnymi przykładami dam już sobię radę

 a to, rozwiaz rownanie :
log3 (2x2 − 5) = 1 bo wiem jak rozwiazac normalne ale nie wiem jak do kwadratu
a to, rozwiaz rownanie :
log3 (2x2 − 5) = 1 bo wiem jak rozwiazac normalne ale nie wiem jak do kwadratu 

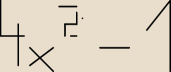 4x
4x
 4x2−1=(2x−1)(2x+1) wzor a2−b2=(a−b)(a+b) i spac
4x2−1=(2x−1)(2x+1) wzor a2−b2=(a−b)(a+b) i spac