narysuj wykres przebiegu funkcji [pilne!!]
UCHO: narysuj wykres przebiegu funkcji f(x)=U{x3}/{x2 − 3} korzystając z 10 punktów:
1. Wyznacz dziedzinę
2. Określ parzystość funkcji
3. Określ miejsce zerowe i p. przecięcia z osią Y
4. Oblicz granice na końcach określoności
5. Równania Asymptot (udowodnij jeśli ich nie ma)
6. Oblicz pochodną i jej miejsce zerowe
7. Oblicz znak pochodnej i wypisz przedziały jej monotoniczności
8. Wyznacz ekstrema funkcji
9. Sporządź tabelkę przebiegu zmienności funkcji
10. Sporządź wykres funkcji
Bardzo pilne! proszę o szczegółowy opis wykonanych czynności. Poziom rozszerzony klasy
maturalnej jak by się kto pytał. Z góry dziękuję tym którym będzie się chciało.
19 lis 00:15
UCHO: Pokażę co mam:
1. z: x
2 − 3 ≠ 0 x
2 ≠ 3 x ≠
√3 v x ≠ −
√3
| | x3 | | x3 | | 0 | |
3. f(x)= |
| 0= |
| f(0)= |
| =0 ← miejsce przecięcia z osią y |
| | x2 − 3 | | x2 −3 | | −3 | |
x
3=0 x=0← miejsce zerowe
| | 3x2(x2−3)−x3*2x | | 3x4−9x2−2x4 | | x4−9x2 | |
6. f'(x)= |
| = |
| = |
| |
| | (x2−3)2 | | x4−6x2+9 | | x4−6x2+9 | |
tu tu się kończy moja praktyczna

6 nie jest skończone a 1 nie wiem czy do końca dobrze.
19 lis 00:30
aniabb: dziedzina ok
2. parzysta jest gdy f(x) = f(−x)
| | (−x)3 | | x3 | |
f(−x) = |
| = − |
| ≠ f(x) funkcja nie jest parzysta |
| | (−x)2−3 | | x2−3 | |
nieparzysta jest gdy f(x) = −f(−x)
| | x3 | | x3 | |
−f(−x) = −(− |
| ) = |
| = f(x) funkcja jest nieparzysta |
| | x2−3 | | x2−3 | |
3.ok
| | x3 | | x | |
4. lim x→−∞ |
| = |
| = −∞ |
| | x2−3 | | 1−3/x2 | |
| | x3 | | −3√3 | |
lim x→−√3 − |
| = |
| = −∞ |
| | x2−3 | | 0+ | |
| | x3 | | −3√3 | |
lim x→−√3 + |
| = |
| = +∞ |
| | x2−3 | | 0− | |
| | x3 | | 3√3 | |
lim x→√3 − |
| = |
| = −∞ |
| | x2−3 | | 0− | |
| | x3 | | 3√3 | |
lim x→√3 + |
| = |
| = +∞ |
| | x2−3 | | 0+ | |
| | x3 | | x | |
lim x→+∞ |
| = |
| = +∞ |
| | x2−3 | | 1−3/x2 | |
5. asymptoty pionowe x=−
√3 i x=
√3
asymptoty poziomej brak (bo lim x→±
∞ = ±
∞)
sprawdzam asymptotę ukośną y=ax+b
| | x3 | | 1 | |
a= lim x→+∞ |
| =lim x→+∞ |
| = 1 |
| | (x2−3)x | | 1−3/x2 | |
| | x3 | | x3 − x3+3x | | 3/x | |
b=lim x→+∞ |
| −1x =lim x→+∞ |
| =lim x→+∞ |
| = 0 |
| | x2−3 | | x2−3 | | 1−3/x2 | |
6. pochodna ok
f'(x)=0 ⇔ x
2(x
2−9) = 0 ⇔ x=0 lub x=−3 lub x=3
7. rysunek
19 lis 07:44
aniabb:
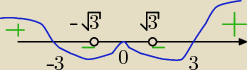
pochodna >0 dla x∊(−
∞;−3) u (3;
∞) funkcja rośnie
pochodna >0 dla x∊(−3;3) \{−
√3;0;
√3} funkcja maleje
8. extremum
f(−3) = −4,5 maksimum (bo przed (−3) rośnie potem maleje)
f(3) = 4,5 minimum (bo przed (3) maleje potem rośnie)
19 lis 07:50
aniabb:
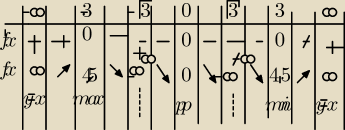
zapomniałam napisać w 8. że w x=0 jest punkt przegięcia
9. Tabelka zmienności ( rys)
19 lis 08:01
aniabb:
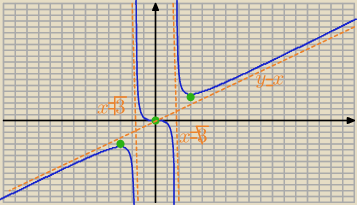
19 lis 08:04
aniabb: wykres
19 lis 08:04
UCHO: ho ho! dzięki

świetne ; ) naprawdę bardzo pomocne ; ) dziękuję

19 lis 13:31
OlOlO: (x4)−(x3)+9
12 gru 17:04
 6 nie jest skończone a 1 nie wiem czy do końca dobrze.
6 nie jest skończone a 1 nie wiem czy do końca dobrze.
 pochodna >0 dla x∊(−∞;−3) u (3;∞) funkcja rośnie
pochodna >0 dla x∊(−3;3) \{−√3;0;√3} funkcja maleje
8. extremum
f(−3) = −4,5 maksimum (bo przed (−3) rośnie potem maleje)
f(3) = 4,5 minimum (bo przed (3) maleje potem rośnie)
pochodna >0 dla x∊(−∞;−3) u (3;∞) funkcja rośnie
pochodna >0 dla x∊(−3;3) \{−√3;0;√3} funkcja maleje
8. extremum
f(−3) = −4,5 maksimum (bo przed (−3) rośnie potem maleje)
f(3) = 4,5 minimum (bo przed (3) maleje potem rośnie)
 zapomniałam napisać w 8. że w x=0 jest punkt przegięcia
9. Tabelka zmienności ( rys)
zapomniałam napisać w 8. że w x=0 jest punkt przegięcia
9. Tabelka zmienności ( rys)

 świetne ; ) naprawdę bardzo pomocne ; ) dziękuję
świetne ; ) naprawdę bardzo pomocne ; ) dziękuję 