Ciągi amsses: Wyznacz największy wyraz ciągu

	2n−16
an=
	n−4,5

w ogóle nie rozumiem tego działu, pomoże ktoś ?

Ajtek: Jaki to poziom?

amsses: tzn?.

Ajtek: Średnia czy studia?

amsses: Średnia

Ajtek: Aha. No to nie mam pomysłu Sprawdź monotoniczność ciągu.

amsses: no właśnie o to chodzi że nie wiem jak to sie robi

aniabb: monotoniczność ..sprawdzasz znak różnicy : a_n+1 − a_n <>0

Ajtek: Policz a_n+1−a_n gdzie:

	2(n+1)−16
an+1=
	(n+1)−4,5

Klos:

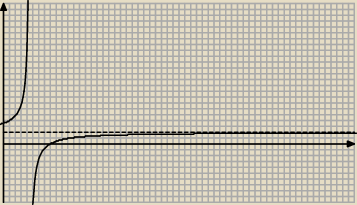
	2x − 16
y =		, wykresem jest hiperbola, na niej leżą wartości ciągu.
	x − 4,5

Największa wartość jest dla n = 4

amsses: Dzieki bardzo

Ajtek: Jest formalny błąd.

	2x−16		2n−16
y=		≠an
	x−4,5		n−4,5

ponieważ dziedziny są różne .

Klos: Jestem tu pierwszy raz. Czy udzielający pomocy to uczniowie?, bo sądząc po wypowiedziach, chyba tak.

Klos:

	2x − 16
Napisałem, że wyrazy ciągu leżą na hiperboli y =		. Coś jest niejasne?
	x − 4,5

Ajtek: No i tak czasem bywa. A jeżeli masz coś do mnie, to napisz gdzie jest mój błąd .

Ajtek: Ciąg ma dziedzinę n∊N₊, natomiast Twoja ilustracja ma x∊R₊. Jest różnica?

Klos: Przemyśl swoją wypowiedź Ajtek. Jeśli mówię, że wyrazy ciągu leżą na hiperboli, to znaczy, że (przypominam określenie ciągu: ciąg to funkcja, której dziedziną jest zbiór liczb naturalnych) dla x naturalnych dodatnich

	2x − 16
(jeśli przyjmiemy, że zero jest liczbą naturalną) wartości funkcji f(x) =
	x − 4,5

	2n − 16
są wyrazami ciągu an =
	n − 4,5

Szkoda czasu na takie tłumaczenia. Dobranoc

Ajtek: Klos, Ty to wiesz i ja to wiem, natomiast uczeń szkoły średniej może nie wiedzieć.

Ajtek: Inaczej, może tego nie rozumieć.

Mila:

	2n−16		2n−9−7
an=		=		=
	n−4,5		(n−4.5)

	2(n−4,5)−7		−7
=		=2+		postać kanoniczna dla funkcji homograficznej ( to masz w
	n−4,5		n−4,5

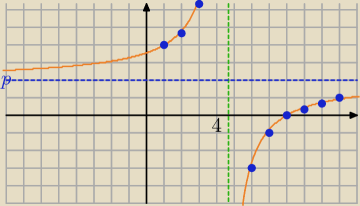
programie LO) funkcja jest rosnąca przedziałami i dla n=4 przyjmie największą wartość (lewa gałązka wykresu) Asymptotą poziomą jest y=2 i z prawej gałązki wykresu możesz odczytać, że a_n<2 odp. a₄ =... oblicz, to największy wyraz tego ciągu.

Ajtek: Hej Mila

Mila: Witam Cię , Ajtku.

Piotr: Witajcie Ajtek, Mila Ajtek nie przejmuj sie

Ajtek: Ja się nie przejmuję Cześć Piotr . Głupot nie napisałem, chyba .

Piotr: nie napisales. a Mila pięknie to narysowala

stawka: A co na to "Bruner" ?

Mila: Witaj Piotrze, narysowałam myśli Ajtka, chyba spać pójdziemy?. Dobranoc, jeszcze pasjansa ułożę i do jutra.

Piotr: to życzę żeby pasjans wyszedł. Dobranoc

Ajtek: Dobrej nocy Mila .