pole kolaaaaa POMOCYYYY!!: w trapezie rownoramiennycm jedna z podstaw jest 2 razy dłuzsza od drugiej, a przekatna jest dwusieczna kata przy dłuzszej podstawie. oblicz dlugosci bokow tego trapezu wiedzac, ze jego pole jest rowne 9cm2. oblicz pole kola opisanego na tym trapezie. +rysunek i obliczonka

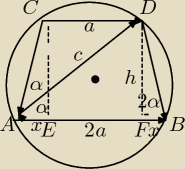
AS: 1. x + a + x = 2*a ⇒ x = a/2 2. AF = x + a = a/2 + a = 3*a/2 3. ΔADF: h/AF = tg(α) ⇒ h = AF*tg(α) = 3*a/2*tg(α) [1] 4. ΔDFB: h/FB = tg(2*α) ⇒ h = FB*tg(2*α) = a/2*tg(2*α) [2] 5. Porównuję h z równań [1] i [2] 3*a/2*tg(α) = a/2*tg(2*α) ⇒ 3*tg(α) = tg(2*α) 6. 2*tg(α) 3*tg(α) = −−−−−−−− Po przemnożeniu przez mianownik 1 − tg²(α) 3*tg(α) − 3*tg³(α) = 2*tg(α) ⇒ 3*tg³(α) − tg(α) = 0 ⇒ tg(α) = 0 lub tg(α) = 1/√3 7. Z ostatniej równości wynika,że α = 30^o 8. DF/AF = tg(α) ⇒ h = 3*a/2*tg(30^o) = 3*a/2*√3/3 = a*√3/2 9. Wyliczam pole trapezu P (= 9 cm²) 0.5*(2*a + a)*h = P ⇒ 3/2*a*a*√3/2 = P ⇒ a² = 4*P/(3*√3) a = 2*√P/(3*√3) 10. Okrąg jest opisany na trójkącie ABD − stąd z tw. sinusów 11. c/sin(α) = 2*R ⇒ R = c/(2*sin(α)) 12. Wystarczy teraz obliczyć c z Δ AFD a następnie pole koła S = π*R²

AS: poprawka do punktu 11 c/sin(2*α) = 2*R ⇒ R = c/(2*sin(2*α))