trapez kaska: w trapezie rownoramiennycm jedna z podstaw jest 2 razy dłuzsza od drugiej, a przekatna jest dwusieczna kata przy dłuzszej podstawie. oblicz dlugosci bokow tego trapezu wiedzac, ze jego pole jest rowne 9cm². oblicz pole kola opisanego na tym trapezie. +rysunek i obliczonka

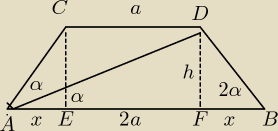
AS: 1. AE + EF + FB = AB ⇒ x + a + x = 2*a ⇒2*x = a ⇒ x = a/2 2. h/AF = tgα ⇒ h = AF*tgα = (a + x)*tgα = 3/2*a*tgα [1] h/FB = tg(2*α) ⇒ h = FB*tgα = a/2*tgα [2] Porównuję h z [1] i [2] 3/2*a*tgα = a/2*tg(2*α) ⇒3*tgα = tg(2*α) 3 Rozwiązuje równanie trygonometryczne 2*tgα 3*tgα = −−−−−−− ⇒ 3*tgα − 3*tg³α = 2*tgα ⇒ 3*tg³α ⇒tgα*(3*tg²α − 1) = 0 1 − tg²α Stąd: tgα = 0 ⇒ α = 0 nie przydatne tgα = −1/√3 odpada,bo kąt będzie rozwarty tgα = 1/√3 spełnia warunki w zadaniu 4 Wysokość trapezu h = 3/2*a*tgα = 3*a/2*1/√3 = 3*a/2*√3/3 = a*√3/2 5 Pole trapezu P = (2a + a)/2*h = 3*a/2*a*√3/2 = 9 z warunku w temacie 3*a²*√3/4 = 9 ⇒ a² = 12/√3 = 12*√3/3 = 4*√3 a = 2*⁴√3 6 Promień koła opisanego na trójkącie ABD (czyli i na trapezie) Z tw. sinusów 2a/sin(180 − 3*α ) = 2*R ⇒ R = a/sin(3*α)