funkcje tryg Arek: Witam. Chciałbym spytać jak rozwiązuje się zadania typu "oblicz wartość funkcji trygonometrycznych" Dla przykładu

	7π		5π
sin(−		−α) i cos(		+α)
	4		2

Nienor: eee

	1		1
−sin(2π−		π+α)=sin(0,25π+α)=		(cosα+sinα)
	4		√2

chyba o ile czegoś nie pomotałam

Arek: ok ale ja nie chciałem rozwiązania bo takie moge znaleźć w książce na końcu. Chciałem się dowiedzieć jak to się robi

Nienor: To nie rozumiem. Znasz wzory redukcyjne Na sin(α+β)

Arek: ok więc ten drugi przykład, =cos(2π+1/2π+α) i jak to dalej zrobić ?

aniabb: https://matematykaszkolna.pl/strona/430.html obrót o 360° czyli 2π nic nie zmienia więc po prostu się to wyrzuca cos(2π+1/2π+α)=cos(1/2π+α) potem kolejne wzory redukcyjne z tabelki cos(1/2π+α) = −sin(α) 6 wzorek w 1 kolumnie

Arek: Dzięki zrobiłem całe zadanko a teraz jeszcze jedno pytanko jak zrobić to: zapisz w postaci funkcji tryg. kąta ostrego

	π
sin(−		)
	3

aniabb: https://matematykaszkolna.pl/strona/430.html pierwszy wzorek 2 akapit sin(−π/3) = −sin(π/3) π/3 = 60° to kąt ostry

Arek: a co jeśli mam cos(9/2π) ?

Aga1.:

9		1
	π=4π+		π
2		2

	1		1
cos(4π+		π)=cos		π=0
	2		2

Arek: a jesli tg(95/3π) to dalej =tg(30π+5/3π) ?

Aga1.: Tg jest funkcją okresową o okresie π

95		2
	π=31π+		π ( 31π wyrzuca się)
3		3

	2		1		1
tg		π=tg(π−		π)=−tg		π=
	3		3		3

Arek: −tg1/3π ?

Aga1.:

	1
(π−		π) która to ćwiartka( mniej niż π, mniej niż 1800), a w tej ćwiartce jaki jest
	3

tangens? Wierszyk znasz?

Arek: nie

Aga1.:

	π
I ćwiartka (0,		)
	2

	π
II ćw. (		,π)
	2

	3
III (π,		π)
	2

	3
IV (		π, 2π)
	2

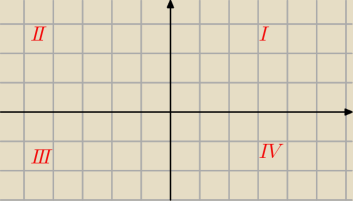
Oto wierszyk W pierwszej ćwiartce wszystkie funkcje są dodatnie w drugiej tylko sinus, w trzeciej tangens i cotangens, a w czwartej cosinus. I tyle.

aniabb: albo po prostu odpowiedni wzorek stąd https://matematykaszkolna.pl/strona/430.html