 Chodzi o wszystkie zadania z tej kartki, oprócz 5, 7 i 3.
http://tinypic.com/r/29n8dq8/6
Chodzi o wszystkie zadania z tej kartki, oprócz 5, 7 i 3.
http://tinypic.com/r/29n8dq8/6
| 4√3 | 1 | 1 | |||
− | * | = | |||
| 2 | 4√3 + 1 | √3 + 1 |
| 4√3 | 4√3 − 1 | |||
− | = | |||
| 2 | (4√3 + 1)(4√3 − 1)(√3+1) |
| 4√3 | 4√3 − 1 | 4√3 − 4√3 + 1 | 1 | ||||
− | = | = | ∊ W | ||||
| 2 | 2 | 2 | 2 |
| 5 | 9 | 3 | ||||
log3/2 12 = log3/2 3 | + 2log9/4 | − log2/3 | ||||
| 9 | 2 | 4 |
| 5 | 9 | 3 | ||||
P = log3/2 3 | + 2log9/4 | − log2/3 | = | |||
| 9 | 2 | 4 |
| 32 |
|
| ||||||||||||||||||||||
log3/2 | + | − | = | |||||||||||||||||||||
| 9 | 2 | −1 |
| 32 | 9 | 3 | ||||
log3/2 [ | * | * | ] = log3/2 12 = L | |||
| 9 | 2 | 4 |
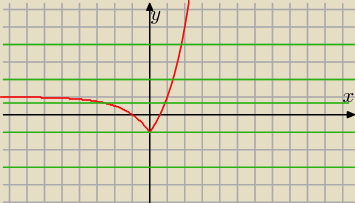 f(x) = |2x+1 − 2| −1
1o Rysujesz 2x
2o Przesuwasz go o wektor [−1;−2]
3o To co znajduje się pod osia OX odbijasz względem osi OX
4o Przesuwasz wykres o wektor [0;−1]
zielone proste oznaczają ilość rozwiązań proste y = m z wykresem f(x)
Brak rozwiązań dla m < −1
Jedno rozwiązanie dla m ∊ {−1} suma <1 ; + ∞)
Dwa rozwiązania dla m ∊ (−1;1)
f(x) = |2x+1 − 2| −1
1o Rysujesz 2x
2o Przesuwasz go o wektor [−1;−2]
3o To co znajduje się pod osia OX odbijasz względem osi OX
4o Przesuwasz wykres o wektor [0;−1]
zielone proste oznaczają ilość rozwiązań proste y = m z wykresem f(x)
Brak rozwiązań dla m < −1
Jedno rozwiązanie dla m ∊ {−1} suma <1 ; + ∞)
Dwa rozwiązania dla m ∊ (−1;1)
| 1 | 1 | 1 | |||
, | , | tworzą ciąg arytmetyczny ⇒ | |||
| log3 2 | log6 2 | log12 2 |

 Jednak mam pare pytań do rozwiązań:
W zadaniu 1) jak zredukowało się wyrażenie pierwiastek 3 + 1 ?
I czy mógłby Pan/Pani bardziej rozpisać lub opisać jak doszło do przekształcenia 2log 9/4 9/2
w zadaniu nr 2.
Jeszcze raz chciałbym podkreślić że jestem bardzo wdzięczny za napisanie rozwiązań!
Jednak mam pare pytań do rozwiązań:
W zadaniu 1) jak zredukowało się wyrażenie pierwiastek 3 + 1 ?
I czy mógłby Pan/Pani bardziej rozpisać lub opisać jak doszło do przekształcenia 2log 9/4 9/2
w zadaniu nr 2.
Jeszcze raz chciałbym podkreślić że jestem bardzo wdzięczny za napisanie rozwiązań! 