Pomocy! Paweł: Krawędzie boczne prawidłowego ostrosłupa trójkątnego są równe a, wysokość zaś jest równa h. Oblicz sinus kąta nachylenia krawędzi bocznej do krawędzi podstawy.

Basia: w kwestii formalnej: krawędzie boczne każdego ostrosłupa prawidłowego są równe wiesz co jest podstawą tego ostrosłupa i w jakim punkcie znajduje się spodek wysokości ?

Paweł: Podstawą jest trójkąt równoboczny. Spodek wysokości znajduje się na przecięciu środkowych. Tak?

Basia: oczywiście no to trójkąt: A(wierzchołek podstawy) S(spodek wysokości) W(wierzchołek ostrosłupa) jest prostokątny szukany kąt to α=∡SAW

	h
sinα =
	a

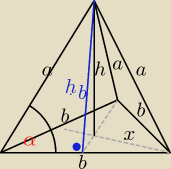
Beti: z tw. Pitagorasa: x² = a² − h² x = √a² − h² w trójkącie równobocznym o boku b:

	2		b√3
x =		*
	3		2

	b√3
x =
	3

b√3 = 3x

	3x
b =		= √3x
	√3

b = √3√a² − h²

	1   b 2
cosα =
	a

	√3√a2 − h2
cosα =
	2a

Paweł: Nie mam takiej odpowiedzi. Są: 1.sinα=^√a2+h2_2a 2.sinα=^√a2+3h2_a 3.sinα=^√a2+2h2_2a 4.sinα=^√a2+3h2_2a

Beti: oo sorry, że się wcisnęłam i zaburzyłam proces twórczego myślenia

Beti: a wogóle to i tak machnęłam się i policzyłam cos zamiast sin, więc musisz liczyć sam

Paweł: Do sinusa potrzebuje hb. Jak ja obliczyć?

Beti: dłuższą część wysokości podstawy oznaczyłam przez 'x'. Krótszą część tej wysokości oznacz np. przez 'y', gdzie:

	1		b√3		b√3
y =		*		=
	3		2		6

a teraz tw. Pitag. do trójkąta prostok. o bokach: y,h,h_b.

Basia: tak jak Ci napisałam

	h
sinα =
	a

cosα = √1−h²/a²

	AS
cosα =
	a

AS = a*√1−h²/a²

	2
AS =		hp
	3

	3
hp =		*a*√1−h2/a2
	2

b − bok podstawy

	b√3
hp =
	2

	2hp		3   2* *a*√1−h2/a2   2
b =		=		=
	√3		√3

3a*√1−h2/a2
	= √3a*√1−h2/a2
√3

h_b liczysz z tw. Pitagorasa

Beti: Basia w zad. chodzi o kąt między kr. boczną a kr. podstawy a nie podstawą