F. kwadratowa fdf: Dla jakich wartości paramatru m rówanie lx² − 4l = m² +1 ma dwa rozwiązania

Mati_gg9225535: x² − 4 = m² + 1 ∨ x² − 4 = − (m² + 1) x² − 4 − m² − 1 = 0 ∨ x² − 4 + m² + 1 = 0 Δ>0 Δ>0

Maslanek: I równości między kolejnymi rozwiązaniami pokazują, że to to samo rozwiązanie (czyli 4 rozwiązania − liczba równości dla danej liczby)

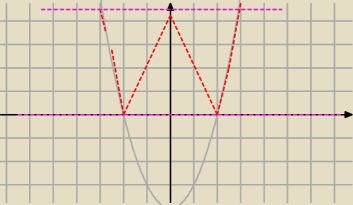
Aga1.: Równanie ma dwa rozwiązania gdy m²+1>4

matt..: zrobiłam tak f(x)= lx²−4l f₁(x)=x²−4 −−>F₂(x)=lx²−4l wyznaczyłam miejsca zerowe x²−4=0 ... (x−2)(x+2)=0 x₁ =2, x₂=−2 p=0 , q=−4 i naryswoałąm wykres.. a nie wiem co zrobić z g(x)=m²+1

fdf: ahaa.. już rozumiem, dzięki za pomoc