logi zombi: Wykaż, że dla dowolnych liczba a,b>0 równanie log ax² + log b = log (ab)^x ma co najmniej jedno rozwiązanie. Kiedy równanie ma jedno rozwiązanie log (abx²) = log (ab)^x /−log (ab)²

	x2
log (		)= 0
	(ab)x−1

x2
	=1
(ab)x−1

x²=(ab)^x−1 Ma dwa rozwiązania to widać bo x²=jakaś dodatnia liczba, pytanie kiedy ma jedno?

Mati_gg9225535: jesli nie popelniles bledu i wykazales ze ma dwa to znaczy również ze ma co najmniej jedno

zombi: A pytanie "Kiedy ma jedno"?

zombi: Dla mnie wygląda tak, że nigdy nie będzie miało jednego ponieważ ab>0 gdyby ab=0 wtedy byloby jedno...

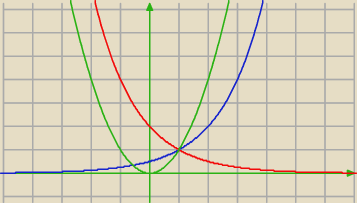
Basia: prawdopodobnie czerwona nigdy po raz drugi nie przetnie zielonej czyli prawdopodobne ⇔ 0 < a*b < 1 ale należałoby to udowodnić

Mati_gg9225535: ale dwa, trzy, cztery,... rozwiazania to to samo co co najmniej jedno

Basia: a przeoczyłam "co najmniej" no to dla każdych a,b∊R takich, że a*b>0

zombi: A czy samo x²=(ab)^x−1 nie wskazuje na to, że ma co najmniej jedno? W końcu lewa strona to kwadrat, a kwadrat ma zawsze dwa rozwiązania, gdy prawa strona jest dodatnia, a tak jest bo ab>0. Natomiast x² ma jedno rozwiazanie, gdy prawa strona =0, dobrze myślę?

zombi: Czyli finał: − Ma co najmniej jedno (jedno lub więcej), ponieważ ma postać x²=(ab)^x−1 gdzie ab>0, zatem ma na pewno dwa rozwiązania, czyli to co mieliśmy pokazać, zostało pokazane. − Nie ma jednego, ponieważ x²≠0, po prawej stronie mamy zawsze dodatnią liczbę.

Basia: 1. to nie są liczby; to są funkcje np. wykresy funkcji f(x) = x² i g(x) = lnx nie mają żadnych punktów wspólnych równanie x² = lnx nie ma rozwiązania analogicznie równanie x² = x²+1 nie ma rozwiązania chociaż funkcja po prawej przyjmują wartości >0 2. nie może być a*b = 0 bo dla a=0 nie istnieje log(ax²) a dla b=0 nie istnieje logb z treści zadania wynika, że ax²>0 ⇔ a>0 i x≠0 b>0 czyli a*b > 0

zombi: Jaka funkcja, przecież na samym początku mam równanie, to samo na końcu. Jak pytają się o ilość rozwiązań w zadaniu to mają na myśli zazwyczaj równanie, nie funkcje. Tym bardziej, że nie napisali, że to jest jakieś f(x)