P.S. Moim zdaniem będzie to 1/4 S, ale mam problem z udowodnieniem.
Rudy102: Trójkąt ABC ma pole równe S. Utworzono nowy trójkąt A'B'C' w taki sposób, że A'=SB(A),
B'=SC(B), oraz C'=SA(C). Oblicz pole trójkąta A'B'C'.
18 lis 11:41
irena_1:
Oznaczyłam:
|AB|=c
|BC|=a
|AC|=b
|< BAC|= α
Wtedy:
|AA'|=2c
|BB'|=2a
|CC'|=2b
| | 1 | | 1 | |
PA'C'A= |
| b*2c sin(1800−α)=2* |
| bc sinα=2PABC=2S |
| | 2 | | 2 | |
Podobnie:
P
A'B'B=2S
P
B'C'C=2S
P
A'B'C'=P
ABC+P
A'C'A+P
A'B'B+P
B'C'C=S+2S+2S+2S=7S
18 lis 12:06
Rudy102:
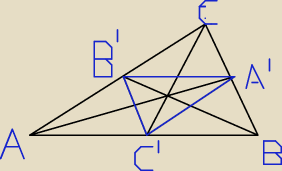
18 lis 12:07
Rudy102: Czyli źle zinterpretowałem polecenie?
18 lis 12:08
irena_1: Można też tak:
Rozważ trójkąty ABC i A'C'A:
− podstawą trójkąta ABC jest bok |AB|=c
− podstawą trójkąta A'C'A jest bok |AA'|=2c
− wysokość trójkąta ABC opuszczona na bok o długości c jest taka sama, jak wysokość trójkąta
A'C'A opuszczona na bok o długości 2c
Stąd− pole trójkąta A'C'A jest 2 razy większe od pola trójkąta ABC
18 lis 12:09
irena_1: Rudy! To chyba nie tak.
Jeśli C'=SAC, to punkt C' jest obrazem punktu C w symetrii względem punktu A. Czyli− punkt A
jest środkiem odcinka CC'.
18 lis 12:10
Rudy102: W zbiorze podają odp 7S, więc miałaś rację dziękuję.
18 lis 12:15
irena_1:
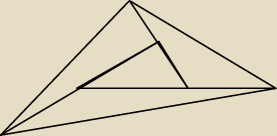
Ten mniejszy trójkąt (w środku) to ABC.
Ten większy to A'B'C'
18 lis 12:15
Rudy102: Tak juz to sam narysowałem Zinterpretowałem symetrię jako środkowe...
18 lis 12:23

 Ten mniejszy trójkąt (w środku) to ABC.
Ten większy to A'B'C'
Ten mniejszy trójkąt (w środku) to ABC.
Ten większy to A'B'C'