Trójkąt prostokątny Jolka: Dane są punkty A(3,2), B(4,7). Na prostej o równaniu x=1 wyznaczyć taki punkt C, że trójkąt ABC jest prostokątny ( kąt przy wierzchołku C ma miare 90 stopni )

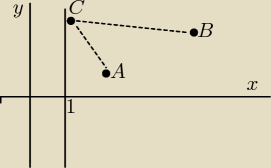
AS: Dane: A(3,2) , B(4,7) , równanie prostej x = 1 Zakładam, że C(1,y) Współczynnik kierunkowy BC mBC =: (yC − yB)/(xC − xB) = (y − 7)/(1 − 4) = (7 − y)/3 Współczynnik kierunkowy AC mAC =: (yC − yA)/(xC − xA) = (y − 2)/(1 − 3) = (2 − y)/2 Warunek prostopadłości: mBC*mAC + 1 = 0 7 − y 2 − y −−−−− * −−−−− + 1 = 0 | *6 3 2 (7 − y)*(2 − y) + 6 = 0 po wymnożeniu i uporządkowaniu y² − 9*y + 20 = 0 po rozwiązaniu równania kwadratowego y1 = 4 , y2 = 5 szukane punkty to: C1(1,4) , C2(1,5)