Rozwiąż równania 2.190 załamana: Rozwiąż równania: a) |x −3| + |x² − 9| = 0 b) |x −1| + |x + 2| + |x − 5| = 0 c) |x + 2| = −1|(x − 2)(x +2)|

Beti: a) można tak: |x−3| + |(x−3)(x+3)| = 0 |x−3| + |x−3||x+3| = 0 |x−3|(1+|x+3|) = 0 |x−3| = 0 lub |x+3| = −1 x = 3 fałsz odp. x = 3

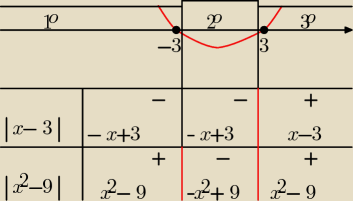
Gustlik: Metoda "osi i tabelki": ad a) |x −3| + |x2 − 9| = 0 Miejsca zerowe modułów: pierwszy moduł x=3, drugi moduł x=3 v x=−3 1) −x+3+x²−9=0 dla x∊(−∞, −3> 2) −x+3−x²+9=0 dla x∊(−3, 3) 3) x−3+x²−9=0 dla x∊<3, +∞) Rozwiąz teraz te 3 przypadki. Pozostałe podobnie.

pigor: ... a b) sprzeczne, bo nie istnieje x takie. że zachodzi równoważność |x −1| + |x + 2| + |x − 5| = 0 ⇔ x−1=0 i x+2=0 i x−5=0 ⇔ x=1 i x=−2 i x=5 , czyli równanie sprzeczne ; c) podobni e jak a) . ...

Beti: b) ponieważ |x| ≥ 0 dla każdego x, a tutaj suma trzech modułów ma dać zero, to byłoby to możliwe tylko wtedy, gdyby istniał taki x, który zerowałby wszystkie moduły jednocześnie. W tym przykładzie jest to niemożliwe, więc odp.: x ∊∅ c) Podobnie: lewa strona równania jest dodatnia (bo jest moduł), a prawa jest ujemna. Strony będą sobie równe tylko wtedy, gdy będą równe zero. Tak będzie tylko w jednym przypadku: dla x = −2, więc odp.: x = −2

pigor: ... , czyli tak jak Beti .oczywiście . ...

pigor: ... a więc z własności iloczynu wartości bezwzględnych |ab|=|a||b| np. tak : c) |x+ 2|= −1|(x−2)(x+2)| ⇔ |x+2|+1|x−2||x+2| =0 ⇔ ⇔ |x+2| (1+|x−2|)= 0 ⇔ x+2=0 lub x∊∅ ⇔ x=−2 . ...